
分析 (1)根据顶点坐标公式,写出顶点坐标,将顶点坐标代入直线解析式即可;
(2)根据题意,用含m的式子表示出点P的坐标,用待定系数法求出抛物线的解析式即可.
解答 解:(1)在抛物线y=-3x2-2x+m中,a=-3,b=-2,c=m,
根据顶点坐标公式,可得顶点坐标为:P($-\frac{1}{3}$,$m+\frac{1}{3}$),
∵点P在直线y=3x+$\frac{7}{3}$上,
∴3×$(-\frac{1}{3})+\frac{7}{3}$=m+$\frac{1}{3}$,解得:m=1,
∴抛物线的解析式为:y=-3x2-2x+1;
(2)如图所示,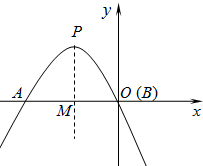
∵PA:PB:AB=1:1:$\sqrt{3}$,
∴△PAB是等腰直角三角形,
∵PM⊥AB,
∴PM=AM=BM,
由抛物线的解析式可知,点P的坐标为($-\frac{1}{3}$,m+$\frac{1}{3}$),
由抛物线具有对称性,可设点A($-\frac{1}{3}-m-\frac{1}{3}$,0),点B($-\frac{1}{3}+m+\frac{1}{3}$,0),即点A($-\frac{2}{3}-m$,0),点B(m,0),
将点A、点B代入抛物线,可得:$\left\{\begin{array}{l}{-3×(-\frac{2}{3}-m)^{2}-2×(-\frac{2}{3}-m)+m=0}\\{-3{m}^{2}-2m+m=0}\end{array}\right.$,解得:m=0或m=$-\frac{1}{3}$,
当m=$-\frac{1}{3}$时,点P($-\frac{1}{3}$,0)在x轴上,不合题意,舍去,
∴m=0,
即抛物线解析式为:y=-3x2-2x.
点评 本题主要考查根据点的特点求抛物线解析式,解决此类问题的关键在于用含有未知数的式子表示坐标,进而用待定系数法求出抛物线解析式.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
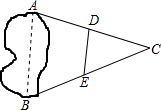 如图,A,B两点分别位于一个池塘的两端,小聪明用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为14m,则A,B间的距离为28m.
如图,A,B两点分别位于一个池塘的两端,小聪明用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为14m,则A,B间的距离为28m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,抛物线y=-$\frac{1}{2}$x2+bx+c经过A,B两点.
如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,抛物线y=-$\frac{1}{2}$x2+bx+c经过A,B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com