
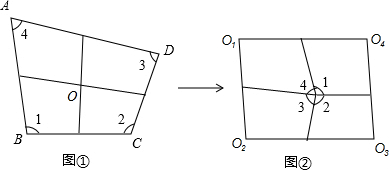
 解:(1)平行四边形,
解:(1)平行四边形,| 1 |
| 2 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 24、如图,有一四边形纸片ABCD,AB∥CD,AD∥BC,∠A=60°,将纸片分别沿折痕MN、PQ折叠,使点A与AB边上的点E重合,点C与CD边上的点F重合,EG平分∠MEB交CD于G,FH平分∠PFD交AB于H.试说明:
24、如图,有一四边形纸片ABCD,AB∥CD,AD∥BC,∠A=60°,将纸片分别沿折痕MN、PQ折叠,使点A与AB边上的点E重合,点C与CD边上的点F重合,EG平分∠MEB交CD于G,FH平分∠PFD交AB于H.试说明:查看答案和解析>>
科目:初中数学 来源: 题型:
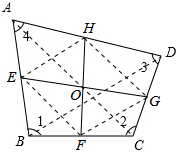
 (2012•河北区三模)如图,一任意四边形纸片ABCD中,E,F,G,H为各边中点,则EG与HF的关系为:①相等;②互相垂直;③互相平分;④垂直平分;⑤相等且垂直.请选择正确序号
(2012•河北区三模)如图,一任意四边形纸片ABCD中,E,F,G,H为各边中点,则EG与HF的关系为:①相等;②互相垂直;③互相平分;④垂直平分;⑤相等且垂直.请选择正确序号查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com