【答案】
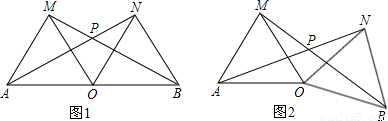
分析:(1)连接MN,先证明四边形MOBN为平行四边形,结合BN=OB,可知平行四边形MOBN为菱形,所以ON⊥BM;
(2)利用(1)中证得的结果四边形MOBN为菱形可知,BM平分∠OBN,又在等边△OBN中,∠OBN=60°,所以∠MBO=30°,即∠PBA=30°,∠PAB=30°,所以∠APB=180°-∠PAB-∠PBA=120°;
(3)①若△OBN绕着点O逆时针旋转α(0°<α<60°)或顺时针旋转α(0°<α<120°)时,∠AON=∠AOM+∠MON=60°+∠MON,∠MOB=∠BON+∠MON=60°+∠MON,可证明△AON≌△MOB,所以∠ONA=∠OBM.则∠APB=ONB+∠ONA+∠OBN-∠OBM=120°.
②若△OBN绕着点O逆时针旋转60°或顺时针旋转120°时,点P与M或O重合,此时仍有∠APB=120°.
③若△OBN绕着点O逆时针旋转α(60°<α<180°)或顺时针旋转α(120°<α<180°)时,类似①可证∠APB=120°.
解答:解:(1)证明:连接MN,∵AO=OB且△OAM和△OBN是等边三角形,
∴OM=BN=OB,∠MOA=∠NBO,(1分)
∴MO∥BN,且OM=BN,
∴四边形MOBN为平行四边形.(3分)
又∵BN=OB,
∴平行四边形MOBN为菱形,
∴ON⊥BM.(4分)
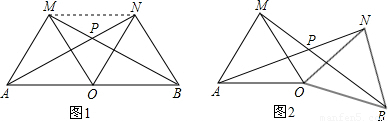
(2)∵四边形MOBN为菱形,
∴BM平分∠OBN,(5分)
又在等边△OBN中,∠OBN=60°,
∴∠MBO=30°,即∠PBA=30°.(6分)
同理∠PAB=30°,
∴∠APB=180°-∠PAB-∠PBA=180°-30°-30°=120°.(8分)
(3)在旋转过程中∠APB大小不发生变化,始终保持120°不变.(9分)
证明:①若△OBN绕着点O逆时针旋转α(0°<α<60°)或顺时针旋转α(0°<α<120°)时,
则如图,在△AON和△MOB中,∠AON=∠AOM+∠MON=60°+∠MON,
又∠MOB=∠BON+∠MON=60°+∠MON,
∴∠AON=∠MOB,(10分)
又AO=MO,ON=OB,
∴△AON≌△MOB,
∴∠ONA=∠OBM.(11分)
∴∠APB=∠ANB+∠PBN=∠ONB+∠ONA+∠OBN-∠OBM=120°.(12分)
②若△OBN绕着点O逆时针旋转60°或顺时针旋转120°时,点P与M或O重合,此时仍有∠APB=120°.(13分)
③若△OBN绕着点O逆时针旋转α(60°<α<180°)或顺时针旋转α(120°<α<180°)时,类似①可证∠APB=120°.(14分)
点评:本题考查旋转的性质,菱形的性质和等边三角形的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要熟练掌握它们的性质,并会熟练地运用全等的性质得到需要的等量关系.