
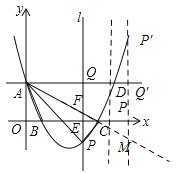
【题目】(14分)如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
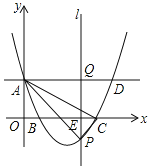
(1)求抛物线的解析式;
(2)当0<t≤8时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)12;(3)t=
;(2)12;(3)t=![]() 或t=
或t=![]() 或t=14.
或t=14.
【解析】试题分析:(1)首先利用根与系数的关系得出: ![]() ,结合条件
,结合条件![]() 求出
求出![]() 的值,然后把点B,C的坐标代入解析式计算即可;(2)(2)分0<t<6时和6≤t≤8时两种情况进行讨论,据此即可求出三角形的最大值;(3)(3)分2<t≤6时和t>6时两种情况进行讨论,再根据三角形相似的条件,即可得解.
的值,然后把点B,C的坐标代入解析式计算即可;(2)(2)分0<t<6时和6≤t≤8时两种情况进行讨论,据此即可求出三角形的最大值;(3)(3)分2<t≤6时和t>6时两种情况进行讨论,再根据三角形相似的条件,即可得解.
试题解析:解:(1)由题意知x1、x2是方程mx2﹣8mx+4m+2=0的两根,
∴x1+x2=8,
由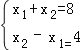 .
.
解得:![]() .
.
∴B(2,0)、C(6,0)
则4m﹣16m+4m+2=0,
解得:m=![]() ,
,
∴该抛物线解析式为:y=![]() ;.
;.
(2)可求得A(0,3)
设直线AC的解析式为:y=kx+b,
∵![]()
∴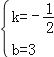
∴直线AC的解析式为:y=﹣![]() x+3,
x+3,
要构成△APC,显然t≠6,分两种情况讨论:
当0<t<6时,设直线l与AC交点为F,则:F(t,﹣![]() ),
),
∵P(t,![]() ),∴PF=
),∴PF=![]() ,
,
∴S△APC=S△APF+S△CPF
=![]()
=![]()
=![]() ,
,
此时最大值为:![]() ,
,
②当6≤t≤8时,设直线l与AC交点为M,则:M(t,﹣![]() ),
),
∵P(t,![]() ),∴PM=
),∴PM=![]() ,
,
∴S△APC=S△APF﹣S△CPF=![]()
=![]()
=![]() ,
,
当t=8时,取最大值,最大值为:12,
综上可知,当0<t≤8时,△APC面积的最大值为12;
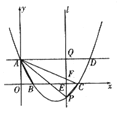
(3)如图,连接AB,则△AOB中,∠AOB=90°,AO=3,BO=2,
Q(t,3),P(t,![]() ),
),
①当2<t≤6时,AQ=t,PQ=![]() ,
,
若:△AOB∽△AQP,则:![]() ,
,
即: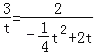 ,
,
∴t=0(舍),或t=![]() ,
,
若△AOB∽△PQA,则:![]() ,
,
即: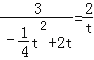 ,
,
∴t=0(舍)或t=2(舍),
②当t>6时,AQ′=t,PQ′=![]() ,
,
若:△AOB∽△AQP,则:![]() ,
,
即: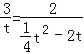 ,
,
∴t=0(舍),或t=![]() ,
,
若△AOB∽△PQA,则:![]() ,
,
即: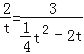 ,
,
∴t=0(舍)或t=14,
∴t=![]() 或t=
或t=![]() 或t=14.
或t=14.


科目:初中数学 来源: 题型:
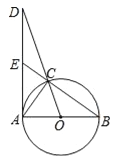
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
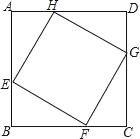
【题目】如图,在正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边上的动点,且AE=BF=CG=DH.
(1)求证:△AEH≌△CGF;
(2)在点E、F、G、H运动过程中,判断直线EG是否经过某一个定点,如果是,请证明你的结论;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小华和小夏玩掷骰子游戏,他们约定:他们用同一枚质地均匀的骰子各掷一次, 如果两次掷的骰子的点数相同则小华获胜:如果两次掷的骰子的点数的和是6则小夏获胜.
(1)请您列表或画树状图列举出所有可能出现的结果;
(2)请你判断这个游戏对他们是否公平并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,∠CAB=30°,DE⊥AC于E,且AE=CE,若DE=5,EB=12,求四边形ABCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
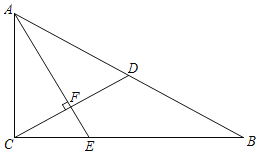
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD于点F,交CB于点E,且∠EAB=∠DCB.
(1)求∠B的度数:
(2)求证:BC=3CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com