
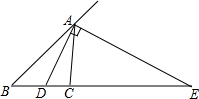
 已知:AD、AE分别为△ABC的内、外角平分线,求证:$\frac{1}{BD}$+$\frac{1}{BE}$=$\frac{2}{BC}$.
已知:AD、AE分别为△ABC的内、外角平分线,求证:$\frac{1}{BD}$+$\frac{1}{BE}$=$\frac{2}{BC}$. 分析 取DE的中点M,连接AM,根据直角三角形斜边上的中线等于斜边的一半,以及等边对等角、三角形外角的性质,证明∠B=∠3,易证△BMA∽△AMC,根据相似三角形的性质:相似三角形的对应边的比相等得到比例式$\frac{AB}{AC}=\frac{AM}{AC}=\frac{BM}{AM}$,然后根据三角形角平分线的性质得到$\frac{AB}{AC}=\frac{BD}{CD}$,等量代换得到$\frac{BM}{AM}=\frac{DB}{CD}$,化简后即可得到结论.
解答  证明:取DE的中点M,连接AM.
证明:取DE的中点M,连接AM.
∵AD、AE分别为三角形ABC的内、外角平分线,
∴∠DAE=90°,
又∵M为DE中点,
∴AM=$\frac{1}{2}$DE=DM,
∴∠MDA=∠MAD=∠2+∠3,
又∵∠MDA=∠1+∠B,
∴∠1+∠B=∠2+∠3,
∵∠1=∠2,
∴∠B=∠3,
又∵∠BMA=∠AMC,
∴△BMA∽△AMC,
∴$\frac{AB}{AC}=\frac{AM}{AC}=\frac{BM}{AM}$,
∵AD是△ABC的角平分线,
∴$\frac{AB}{AC}=\frac{BD}{CD}$,
∴$\frac{BM}{AM}=\frac{DB}{CD}$,
∴$\frac{BD+DM}{AM}=\frac{BD}{BC-BD}$,
∴$\frac{BD}{\frac{1}{2}DE}+1=\frac{BD}{BC-BD}$
$\frac{DB}{\frac{1}{2}(BE-BD)}+1=\frac{BD}{BC-BD}$,
化简得BE•BC+BD•BC=2BD•BE,
等式两边同除以(BE•BC•BD)得:$\frac{1}{BD}$+$\frac{1}{BE}$=$\frac{2}{BC}$.
点评 本题考查了直角三角形的性质,以及相似三角形的判定与性质,三角形角平分线的性质,正确证明△BMA∽△AMC是关键.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
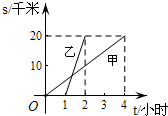 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )| A. | 甲的速度是4千米/小时 | B. | 乙的速度是10千米/小时 | ||
| C. | 乙比甲晚出发1小时 | D. | 甲比乙晚到B地3小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.则这组数据的中位数是30.
如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.则这组数据的中位数是30.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com