
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
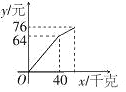
【答案】(1)y=1.6x;(2)50千克;(3)36元
【解析】
(1)设y与x的函数关系式为y=kx,把已知坐标代入解析式可解;
(2)降价前西瓜售价每千克1.6元.降价0.4元后西瓜售价每千克1.2元,故可求出降价后销售的西瓜,从而问题得解;
(3)用销售总金额减去购西瓜的费用即可求得利润.
(1)设关系式是y=kx,把x=40,y=64代入得40k=64,解得k=1.6,
则关系式是y=1.6x;
(2)因为降价前西瓜售价为每千克1.6元,
所以降价0.4元后西瓜售价每千克1.2元,
降价后销售的西瓜为(76- 64)÷1.2=10(千克),所以小明从批发市场共购进50千克西瓜;
(3)76- 50×0.8=76- 40=36(元),即小明这次卖西瓜赚了36元钱.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】一套三角尺(分别含![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() 的角)按如图所示摆放在量角器上,边
的角)按如图所示摆放在量角器上,边![]() 与量角器
与量角器![]() 刻度线重合,边
刻度线重合,边![]() 与量角器
与量角器![]() 刻度线重合,将三角尺
刻度线重合,将三角尺![]() 绕量角器中心点
绕量角器中心点![]() 以每秒
以每秒![]() 的速度顺时针旋转,当边
的速度顺时针旋转,当边![]() 与
与![]() 刻度线重合时停止运动,设三角尺
刻度线重合时停止运动,设三角尺![]() 的运动时间为
的运动时间为![]() .
.
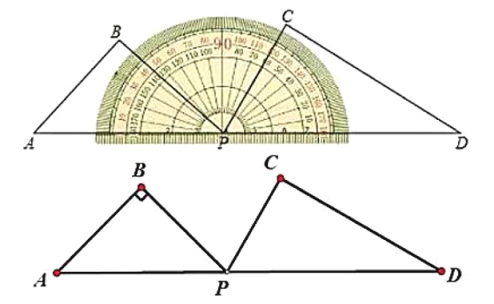
(1)当![]() 时,边
时,边![]() 经过的量角器刻度线对应的度数是 度;
经过的量角器刻度线对应的度数是 度;
(2)若在三角尺![]() 开始旋转的同时,三角尺
开始旋转的同时,三角尺![]() 也绕点
也绕点![]() 以每秒
以每秒![]() 的速度逆时针旋转,当三角尺
的速度逆时针旋转,当三角尺![]() 停止旋转时,三角尺
停止旋转时,三角尺![]() 也停止旋转.
也停止旋转.
①当![]() 为何值时,边
为何值时,边![]() 平分
平分![]() ;
;
②在旋转过程中,是否存在某一时刻使![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援四川抗震救灾,某省某市A、B、C三地分别有赈灾物资100吨、100吨、80吨,需要全部运往四川重灾区的甲、乙两县.根据灾区的情况,这批赈灾物资运往甲县的数量比运往乙县的数量的2倍少20吨.
(1)求这批赈灾物资运往甲、乙两县的数量各是多少吨?
(2)若要求C地运往甲县的赈灾物资为60吨,A地运往甲县的赈灾物资为x吨(x为整数),B地运往甲县的赈灾物资数量少于A地运往甲县的赈灾物资数量的2倍,其余的赈灾物资全部运往乙县,且B地运往乙县的赈灾物资数量不超过25吨.则A、B两地的赈灾物资运往甲、乙两县的方案有几种?
(3)已知A、B、C三地的赈灾物资运往甲、乙两县的费用如表:
A地 | B地 | C地 | |
运往甲县的费用(元/吨) | 220 | 200 | 200 |
运往乙县的费用(元/吨) | 250 | 220 | 210 |
为及时将这批赈灾物资运往甲、乙两县,某公司主动承担运送这批物资的总费用,在(2)的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.
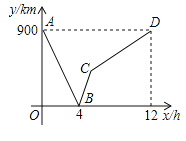
(1)甲、乙两地之间的距离为 千米;图中点B的实际意义是 ;
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠DAE=∠BCF.
(1)试判断直线AE与CF有怎样的位置关系?并说明理由;
(2)若∠BCF=70°,求∠ADF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com