
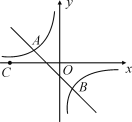
【题目】如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出,当kx+b<![]() 时,x的取值范围;
时,x的取值范围;
(3)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
【答案】(1)反比例函数的解析式为![]() ,一次函数的解析式为
,一次函数的解析式为![]() ;(2)
;(2)![]() 或
或![]() ;(3)C点坐标为(-5,0),t的最大值为
;(3)C点坐标为(-5,0),t的最大值为![]() .
.
【解析】
(1)先将点![]() 代入反比例函数可求出其解析式,从而可得点A的坐标,再利用待定系数法可求出一次函数的解析式;
代入反比例函数可求出其解析式,从而可得点A的坐标,再利用待定系数法可求出一次函数的解析式;
(2)根据点A、B的坐标,利用图象法求解即可得;
(3)如图(见解析),作点A关于x轴的对称点![]() ,从而可得点
,从而可得点![]() 的坐标,再根据三角形的三边关系定理得出t取得最大值时,点
的坐标,再根据三角形的三边关系定理得出t取得最大值时,点![]() 的位置,然后利用两点之间的距离公式可求出t的最大值,又利用待定系数法求出直线
的位置,然后利用两点之间的距离公式可求出t的最大值,又利用待定系数法求出直线![]() 的解析式,再令
的解析式,再令![]() 可求出点C的坐标.
可求出点C的坐标.
(1)将点![]() 代入反比例函数
代入反比例函数![]() 得:
得:![]() ,解得
,解得![]()
则反比例函数的解析式为![]()
当![]() 时,
时,![]() ,即点
,即点![]()
将![]() ,
,![]() 代入一次函数的解析式得:
代入一次函数的解析式得:![]()
解得![]()
则一次函数的解析式为![]() ;
;
(2)![]() 表示的是一次函数的图象位于反比例函数图象的下方,求出此时的x取值范围即可
表示的是一次函数的图象位于反比例函数图象的下方,求出此时的x取值范围即可
则结合![]() ,
,![]() 可得:
可得:![]() 或
或![]()
故x的取值范围为![]() 或
或![]() ;
;
(3)如图,作点A关于x轴的对称点![]()
则点![]() 的坐标为
的坐标为![]() ,
,![]()
因此有![]()
由三角形的三边关系定理得:![]()
当且仅当![]() 三点共线时,t取得最大值,最大值为
三点共线时,t取得最大值,最大值为![]()
由两点之间的距离公式得:![]()
即t的最大值为![]()
设直线![]() 的解析式为
的解析式为![]()
将![]() ,
,![]() 代入得:
代入得:![]()
解得
则直线![]() 的解析式为
的解析式为![]()
令![]() 得
得![]() ,解得
,解得![]()
则点C的坐标为![]() .
.



 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
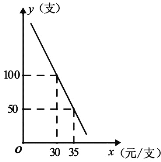
【题目】某网店专售一品牌牙膏,其成本为22元/支,销售中发现,该商品每天的销售量![]() (支)与销售单价
(支)与销售单价![]() (元/支)之间存在如图所示的关系.
(元/支)之间存在如图所示的关系.
(1)请求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)该品牌牙膏销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)在武汉爆发“新型冠状病毒”疫情期间,该网店店主决定从每天获得的利润中抽出100元捐赠给武汉,为了保证捐款后每天剩余的利润不低于350元,在抗“新型冠状病毒”疫情期间,市场监督管理局加大了对线上、线下商品销售的执法力度,对商品售价超过成本价的20%的商家进行处罚,请你给该网店店主提供一个合理化的销售单价范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC,BC交于点E,F. 过点F作⊙O的切线交AB于点M.

(1)求证:MF⊥AB;
(2)若⊙O的直径是6,填空:
①连接OF,OM,当FM= 时,四边形OMBF是平行四边形;
②连接DE,DF,当AC= 时,四边形CEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 的另一个交点为
的另一个交点为![]() .
.
(1)求![]() 的值和抛物线的解析式;
的值和抛物线的解析式;
(2)点![]() 在抛物线上,且点
在抛物线上,且点![]() 的横坐标为
的横坐标为![]() (
(![]() ).
).![]() 轴交直线
轴交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,且四边形
上,且四边形![]() 为矩形(如图2),若矩形
为矩形(如图2),若矩形![]() 的周长为
的周长为![]() ,求
,求![]() 与
与![]() 的函数关系式以及
的函数关系式以及![]() 的最大值;
的最大值;
(3)![]() 是平面内一点,将
是平面内一点,将![]() 绕点
绕点![]() 沿逆时针方向旋转
沿逆时针方向旋转![]() 后,得到
后,得到![]() ,点
,点![]() 、
、![]() 、
、![]() 的对应点分别是点
的对应点分别是点![]() 、
、![]() 、
、![]() .若
.若![]() 的两个顶点恰好落在抛物线上,请直接写出点
的两个顶点恰好落在抛物线上,请直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
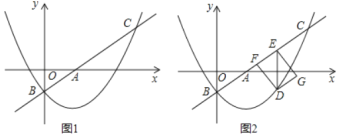
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,
,![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 在抛物线上,
在抛物线上,![]() 轴,且
轴,且![]() .
.
(1)求点![]() ,
,![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)点![]() 为
为![]() 轴右侧抛物线上一点.
轴右侧抛物线上一点.
①如图①,若![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,求点
,求点![]() 的坐标;
的坐标;
②如图②,抛物线上一点![]() 的横坐标为2,直线
的横坐标为2,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
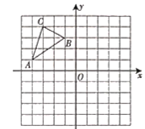
【题目】在边长为1的小正方形组成的网格中建立如图所示的平面直角坐标系,![]() 是格点三角形(顶点是网格线的交点).
是格点三角形(顶点是网格线的交点).
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)画出![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 得到的
得到的![]() ;
;
(3)在(2)的条件下,![]() 点所经过的路径长为 (结果保留
点所经过的路径长为 (结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
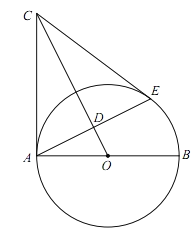
【题目】已知:如图,AB是⊙O的直径,点C是过点A的⊙O的切线上一点,连接OC,过点A作OC的垂线交OC于点D,交⊙O于点E,连接CE.
(1)求证:CE与⊙O相切;
(2)连结BD并延长交AC于点F,若OA=5,sin∠BAE=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
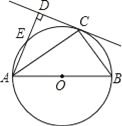
【题目】如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com