
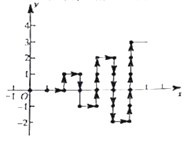
【题目】如图,在平面直角坐标系中,有若千个整数点,其顺序按图中“![]() ”方向排列,如
”方向排列,如![]() ….根据这个规律探索可得,第
….根据这个规律探索可得,第![]() 个点的坐标为__________.
个点的坐标为__________.
科目:初中数学 来源: 题型:
【题目】在有理数范围内,我们定义三个数之间的新运算“![]() ”法则:a
”法则:a![]() b
b![]() c=|a+b+c|-a+b-c,例如:1
c=|a+b+c|-a+b-c,例如:1![]() 2
2![]() (-3)=|1+2+(-3)|-1+2-(-3)=4.在
(-3)=|1+2+(-3)|-1+2-(-3)=4.在![]() 这6个数中,任意取三个数作为a、b、c的值,则a
这6个数中,任意取三个数作为a、b、c的值,则a![]() b
b![]() c的最大值为___________
c的最大值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为
点对应的数为![]() ,
,![]() 点对应的数为
点对应的数为![]() .
.
![]()
(1)请写出与![]() 、
、![]() 两点距离相等的点
两点距离相等的点![]() 所对应的数;
所对应的数;
(2)现有一只电子蚂蚁![]() 从
从![]() 点出发,以
点出发,以![]() 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以
点出发,以![]() 单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,你知道
点相遇,你知道![]() 点对应的数是多少吗?(写出计算过程)
点对应的数是多少吗?(写出计算过程)
(3)在题(2)中,若运动t秒钟时,两只蚂蚁的距离为10,求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
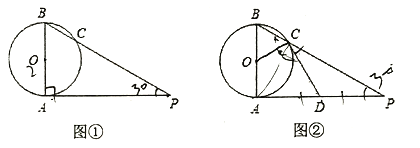
【题目】己知AB是⊙0的直径,AP是⊙0的切线,A是切点,BP与⊙0交于点C.
(1)如图①,若AB=2,∠P=30![]() ,求AP的长.(结果保留根号)
,求AP的长.(结果保留根号)
(2)如图②,若D为AP的中点,∠P=30![]() ,求证:直线CD是⊙O的切线.
,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
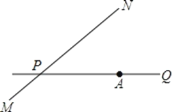
【题目】如图,公路 MN 和公路 PQ 在点 P 处交会,且∠QPN=30°.点 A 处有一所中学,AP=160m,一辆拖拉机从 P 沿公路 MN 前行,假设拖拉机行驶时周围 100m 以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响,已知拖拉机的速度为 18km/h,那么学校受影响的时间为多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
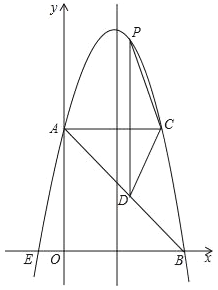
【题目】如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
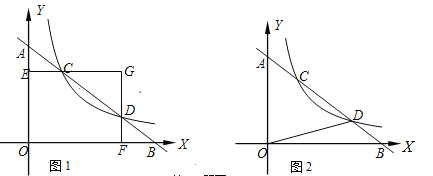
【题目】探究:如图1 ,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数![]() 的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
(1)若![]() ,请用含n的代数式表示
,请用含n的代数式表示![]() ;
;
(2)求证: ![]() ;
;
应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数![]() 的图象交于点C,D两点(点C在点D的左边),已知
的图象交于点C,D两点(点C在点D的左边),已知![]() ,△OBD的面积为1,试用含m的代数式表示k.
,△OBD的面积为1,试用含m的代数式表示k.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com