
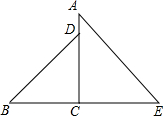
 如图所示 AC⊥BE垂足为C,BD=AE,CD=CE,请探索直线BD与直线AE的位置关系.
如图所示 AC⊥BE垂足为C,BD=AE,CD=CE,请探索直线BD与直线AE的位置关系. 解:直线BD与直线AE的位置关系是:垂直.理由如下:
解:直线BD与直线AE的位置关系是:垂直.理由如下:
|


科目:初中数学 来源: 题型:
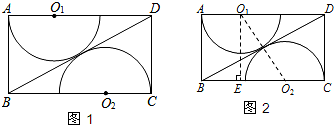 问题:如图1,要在一个矩形木板ABCD上切割、拼接出一个圆形桌面,可在该木板上切割出半径相等的半圆形O1和半圆形O2,其中O1、O2分别是AD、BC上的点,半圆O1分别与AB、BD 相切,半圆O2分别与CD、BD相切.若AB=am,BC=bm,求最终拼接成的圆形桌面的半径(用含a、b的代数式表示).
问题:如图1,要在一个矩形木板ABCD上切割、拼接出一个圆形桌面,可在该木板上切割出半径相等的半圆形O1和半圆形O2,其中O1、O2分别是AD、BC上的点,半圆O1分别与AB、BD 相切,半圆O2分别与CD、BD相切.若AB=am,BC=bm,求最终拼接成的圆形桌面的半径(用含a、b的代数式表示).| a2+b2 |
| 4b |
| a2+b2 |
| 4b |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| A、两条射线组成的图形叫做角 |
| B、周角是一条射线 |
| C、在直线上任取一点作顶点,就可以把这条直线看作一个平角 |
| D、在∠AOB的边OB的延长线上任取一点D |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com