
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=![]() ,连接PB,试探究PA、PB、PC满足的等量关系.
,连接PB,试探究PA、PB、PC满足的等量关系.
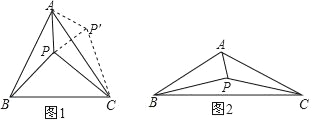
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为 度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为 ;
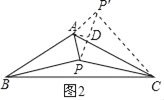
(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
(3)PA、PB、PC满足的等量关系为 .
【答案】(1)150,PA2+PC2=PB2;(2)3PA2+PC2=PB2;(3)4PA2sin2![]() +PC2=PB2
+PC2=PB2
【解析】试题分析:(1)根据旋转变换的性质得到△PAP′为等边三角形,得到∠P′PC=90°,根据勾股定理解答即可;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,作AD⊥PP′于D,根据余弦的定义得到PP′=![]() PA,根据勾股定理解答即可;
PA,根据勾股定理解答即可;
(3)与(2)类似,根据旋转变换的性质、勾股定理和余弦、正弦的关系计算即可.
试题解析:
(1)∵△ABP≌△ACP′,
∴AP=AP′,
由旋转变换的性质可知,∠PAP′=60°,P′C=PB,
∴△PAP′为等边三角形,
∴∠APP′=60°,
∵∠PAC+∠PCA=![]() =30°,
=30°,
∴∠APC=150°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∴PA2+PC2=PB2,
故答案为:150,PA2+PC2=PB2;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=120°,P′C=PB,
∴∠APP′=30°,
∵∵∠PAC+∠PCA=![]() =60°,
=60°,
∴∠APC=120°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=30°,
∴PD=![]() PA,
PA,
∴PP′=![]() PA,
PA,
∴3PA2+PC2=PB2;
(3)如图2,与(2)的方法类似,
作将△ABP绕点A逆时针旋转α得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=α,P′C=PB,
∴∠APP′=90°﹣![]() ,
,
∵∵∠PAC+∠PCA=![]() ,
,
∴∠APC=180°﹣![]() ,
,
∴∠P′PC=(180°﹣![]() )﹣(90°﹣
)﹣(90°﹣![]() )=90°,
)=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=90°﹣![]() ,
,
∴PD=PAcos(90°﹣![]() )=PAsin
)=PAsin![]() ,
,
∴PP′=2PAsin![]() ,
,
∴4PA2sin2![]() +PC2=PB2,
+PC2=PB2,
故答案为:4PA2sin2![]() +PC2=PBspan>2.
+PC2=PBspan>2.


科目:初中数学 来源: 题型:
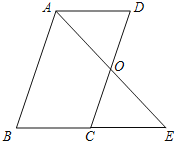
【题目】已知:如图,□ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
![]() 求证:
求证: ![]() ≌
≌![]() ;
;
![]() 连接
连接![]() ,当
,当![]() ______°和
______°和![]() ______°时,四边形ACED是正方形?请说明理由.
______°时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)“中国梦”关系每个人的幸福生活,为展现巴中人追梦的风采,我市某中学举行“中国梦我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.

(1)参加比赛的学生人数共有 名,在扇形统计图中,表示“D等级”的扇形的圆心角为 度,图中m的值为 ;
(2)补全条形统计图;
(3)组委会决定从本次比赛中获得A等级的学生中,选出2名去参加市中学生演讲比赛,已知A等级中男生有1名,请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)利用求根公式计算,结合①②③你能得出什么猜想?
①方程x2+2x+1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
②方程x2-3x-1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
③方程3x2+4x-7=0的根为x1=_______,x2=________,x1+x2=________,x1·x2=________.
(2)利用求根公式计算:一元二次方程ax2+bx+c=0(a≠0,且b2-4ac≥0)的两根为x1=________,x2=________,x1+x2=________,x1·x2=________.
(3)利用上面的结论解决下面的问题:
设x1、x2是方程2x2+3x-1=0的两个根,根据上面的结论,求下列各式的值:
①![]() ; ②
; ②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲.乙两人进行跑步训练,他们所跑的路程y(米)与时间x(秒)之间的关系如图所示,则下列说法错误的是( )

A. 离终点40米处,乙追上甲B. 甲比乙迟3秒到终点
C. 甲跑步的速度是5米/秒D. 乙跑步的速度是![]() 米/秒
米/秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图①,数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如,线段AB=0﹣(﹣1)=1:线段:BC=2﹣0=2;线段AC=2﹣(﹣1)=3(大的数减去小的数).
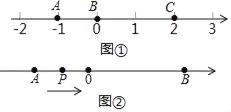
(1)数轴上点A、B表示的数分别是﹣3和2,则AB= ;
(2)数轴上点M表示的数是﹣1,线段MN的长为2,则点N表示的数是 ;
(3)如图②,数轴上点A、B表示的数分别是﹣4和6,动点P从点A出发,沿AB方向以每秒2个单位长度的速度运动,点P运动多少秒时BP=4.并求此时点P表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )
(1)乙车的速度为80km/h(千米/小时);(2)a=40,m=1;(3)甲车共行驶了7h;(4)乙车一定行驶了![]() h或
h或![]() h,两车恰好距离50km.
h,两车恰好距离50km.

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() ,
,![]() ,把矩形
,把矩形![]() 沿直线
沿直线![]() 对折使点
对折使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在坐标平面内,若四边形
在坐标平面内,若四边形![]() 是菱形,则菱形
是菱形,则菱形![]() 的面积是( )
的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1,AA2,AA3…,依此作法,则∠AAnAn+1等于______度.(用含n的代数式表示,n为正整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com