
【题目】在平面直角坐标系中,点A(0,a)、B(b,0).
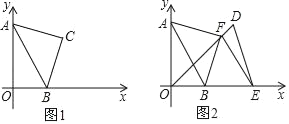
(1)若a、b满足a2+b2﹣8a﹣4b+20=0.如图,在第一象限内以AB为斜边作等腰Rt△ABC,请求四边形AOBC的面积S;
(2)如图,若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF,判断AF与BF的关系,并说明理由.
【答案】(1)9;(2) 结论:FA=FB,FA⊥FB,理由见解析.
【解析】
(1)根据非负数的性质列出算式,求出a、b的值;根据等腰直角三角形的性质求出AC、BC,根据三角形的面积公式计算即可;
(2)作FG⊥y轴,FH⊥x轴垂足分别为G、H,证明四边形FHOG是正方形,得到OG=FH,∠GFH=90°,证明△AFG≌△BFH,根据全等三角形的性质计算即可.
解:(1)∵a2+b2-8a-4b+20=0,
∴(a-4)2+(b-2)2=0,
∴a=4,b=2;即A(0,4),B(2,0),
∴AB=![]() =2
=2![]()
∵△ABC是等腰直角三角形,
∴AC=BC=![]() ,
,
∴四边形AOBC的面积S=![]() ×OA×OB+
×OA×OB+![]() ×AC×BC=4+5=9;
×AC×BC=4+5=9;
(2)
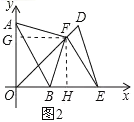
结论:FA=FB,FA⊥FB,理由如下:
如图2,作FG⊥y轴,FH⊥x轴垂足分别为G、H,
∵A(0,a)向右平移a个单位到D,
∴点D坐标为(a,a),点E坐标为(a+b,0),
∴∠DOE=45°,
∵EF⊥OD,
∴∠OFE=90°,∠FOE=∠FEO=45°,
∴FO=EF,
∴FH=OH=HE=![]() (a+b),
(a+b),
∴点F坐标为(![]() ,
,![]() ),
),
∴FG=FH,四边形FHOG是正方形,
∴OG=FH=![]() ,∠GFH=90°,
,∠GFH=90°,
∴AG=AO-OG=a-![]() =
=![]() ,BH=OH-OB=
,BH=OH-OB=![]() -b=
-b=![]() ,
,
∴AG=BH,
在△AFG和△BFH中,
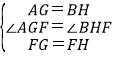
∴△AFG≌△BFH,
∴FA=FB,∠AFG=∠BFH,
∴∠AFB=∠AFG+∠BFG=∠BFH+∠BFG=90°,
∴FA=FB,FA⊥FB.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
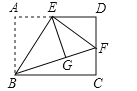
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F. 若AB=6,BC=![]() ,则FD的长为( )
,则FD的长为( )
A. 2B. 4C. 6D. 23
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是计算机中的一种益智小游戏“扫雷”的画面,在一个![]() 的小方格的正方形 雷区中,随机埋藏着
的小方格的正方形 雷区中,随机埋藏着![]() 颗地雷,每个小方格内最多只能埋藏
颗地雷,每个小方格内最多只能埋藏![]() 颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“
颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“![]() ”,其意义表示该格的外围区域(图中阴影部分,记为
”,其意义表示该格的外围区域(图中阴影部分,记为![]() 区域)有
区域)有![]() 颗地雷;接着小红又点击了左上角第一个方格,出现了数字“
颗地雷;接着小红又点击了左上角第一个方格,出现了数字“![]() ”,其外围区域(图中阴影)记为
”,其外围区域(图中阴影)记为![]() 区域;
区域;![]() 区域与
区域与![]() 区域以及出现数字“
区域以及出现数字“![]() ”和“
”和“![]() ”两格以外的部分记为
”两格以外的部分记为![]() 区域。请分别计算出
区域。请分别计算出![]() 区、
区、![]() 区、
区、![]() 区点中地雷的概率,那么她应点击
区点中地雷的概率,那么她应点击![]() 、
、![]() 、
、![]() 中的哪个区域?
中的哪个区域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的角平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.
(1)求证:E是AD中点;
(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在直角坐标系中,
在直角坐标系中,

(1)请写出![]() 顶点在第一象限内的坐标;
顶点在第一象限内的坐标;
(2)若把![]() 向上平移
向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度得到
个单位长度得到![]() ,画出平移后的图形;
,画出平移后的图形;
(3)求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB的高为16m,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为 60°,在楼顶B处测得塔顶D处的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高.(![]() =1.73,结果保留一位小数.)
=1.73,结果保留一位小数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
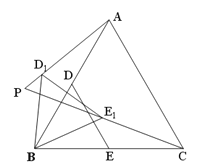
【题目】已知:在等边△ABC中, AB=![]() , D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
, D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com