
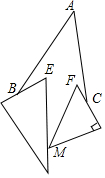
 如图,已知两块三角板如图摆放,点B和点C分别在两块三角板的边上,一块三角板的顶点M在另一块三角板的边上,且∠BAC=40°,∠E=60°,∠F=45°,则∠ABE+∠EMF+∠FCA=65 度.
如图,已知两块三角板如图摆放,点B和点C分别在两块三角板的边上,一块三角板的顶点M在另一块三角板的边上,且∠BAC=40°,∠E=60°,∠F=45°,则∠ABE+∠EMF+∠FCA=65 度. 分析 延长BE交AC于D,延长CF交BD于G,根据外角的性质得到∠EGF=∠BDC+∠ACF=∠A+∠ABE+∠ACF,根据四边形的内角和和邻补角的定义得到∠ABE+∠EMF+∠FCA+∠A=∠BEM+∠CFM=105°,于是得到结论.
解答  解:延长BE交AC于D,延长CF交BD于G,
解:延长BE交AC于D,延长CF交BD于G,
∵∠BDC=∠A+∠ABE,
∠EGF=∠BDC+∠ACF=∠A+∠ABE+∠ACF,
∴∠ABE+∠EMF+∠FCA+∠A=∠BEM+∠CFM=105°,
∴∠ABE+∠EMF+∠FCA=105°-∠A=65°,
故答案为:65.
点评 本题考查了三角形的外角的性质,四边形的内角和,邻补角的定义,熟练掌握三角形的外角的性质是解题的关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:填空题
 如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2013为$\frac{α}{{2}^{2012}}$.
如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2013为$\frac{α}{{2}^{2012}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.35×1010元 | B. | 3.5×108元 | C. | 3.5×109元 | D. | 35×108元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
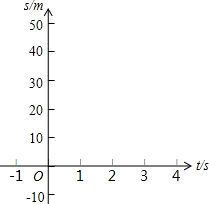 一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)
一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)| 滑行时间t/s | 0 | 1 | 2 | 3 | 4 |
| 滑行距离s/m | 0 | 4.5 | 14 | 28.5 | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
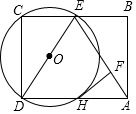 如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F.
如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com