

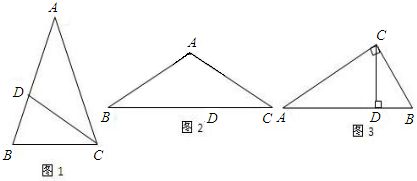
 解:(1)如图所示:
解:(1)如图所示:

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
| ||
| 2 |
| AB |
| BC |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源:同步轻松练习 八年级 数学 上 题型:044
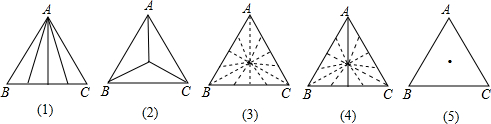
如图,是我们熟悉的图形之一,这个图形可以看做是按一定规则连接正五边形的顶点得到的,被称为正五角星,这个图形有几条对称轴?在这个图形中有哪些等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年数学参赛试卷2010.3吴(解析版) 题型:解答题
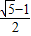 ,底角平分线与腰的交点为黄金分割点.
,底角平分线与腰的交点为黄金分割点.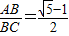 ,则请你求出∠A的度数;
,则请你求出∠A的度数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com