
【题目】在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你补全证明过程:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:EF∥CD

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正△ABC中,D,E分别在AC,AB上,且 ![]() ,AE=BE,则有( )
,AE=BE,则有( )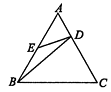
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图象经过坐标原点,与x轴的另一个交点为A(-2,0).
的图象经过坐标原点,与x轴的另一个交点为A(-2,0).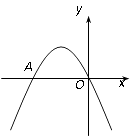
(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决下列问题:
材料一:对非负实数x“四舍五入”到个位的值记为![]() ,即:当n为非负整数时,如果
,即:当n为非负整数时,如果![]() ,则
,则![]() ;反之,当n为非负整数时,如果
;反之,当n为非负整数时,如果![]() ;则
;则![]() ,例如:
,例如:![]() ,
,![]() ,
,![]() ,
,![]()
材料二:平面直角坐标系中任意两点![]() ,
,![]() ,我们把
,我们把![]() 叫做
叫做![]() 、
、![]() 两点间的折线距离,并规定
两点间的折线距离,并规定![]() 若
若![]() 是一定点,
是一定点,![]() 是直线
是直线![]() 上的一动点,我们把
上的一动点,我们把![]() 的最小值叫做
的最小值叫做![]() 到直线
到直线![]() 的折线距离,例如:若
的折线距离,例如:若![]() ,
,![]() 则
则![]() .
.
![]() 如果
如果![]() ,写出实数x的取值范围;
,写出实数x的取值范围;![]() 已知点
已知点![]() ,点
,点![]() ,且
,且![]() ,求a的值.
,求a的值.
![]() 若m为满足
若m为满足![]() 的最大值,求点
的最大值,求点![]() 到直线
到直线![]() 的折线距离.
的折线距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 ![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= ![]() .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com