
如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分 别为A(0,2),D(2,2),AB=2
别为A(0,2),D(2,2),AB=2 ,连接AC.
,连接AC.
(1)求出直线AC 的函数解析式;
的函数解析式;
(2)求过点A,C,D的抛物线的函数解析式;
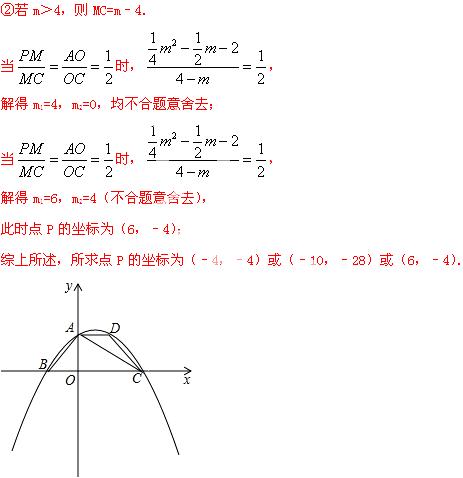
(3)在抛物线上有一点P(m,n)(n<0),过点P作PM垂直于x轴,垂足为M,连接PC,使以点C,P,M为顶点的三角形与Rt△AOC相似,求出点P的坐标.


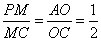 时,列出方程
时,列出方程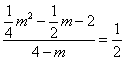 ,解方程求出m的值均不合题意舍去;由
,解方程求出m的值均不合题意舍去;由 ,列出方程
,列出方程 ,解方程求出m的值,得到点P的坐标为(6,﹣4
,解方程求出m的值,得到点P的坐标为(6,﹣4 ).
).
试题解析:(1)由A(0,2)知OA=2,
在Rt△ABO中,∵∠AOB=90°,AB=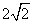 ,
,

∴y=- x2+
x2+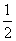 x+2;
x+2;
(3)∵点P(m,n)(n<0)在抛物线y=- x2+
x2+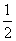 x+2上,
x+2上,
∴m<﹣2或m>4,n=﹣ m2+
m2+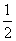 m+2<0,
m+2<0,
∴PM= m2﹣
m2﹣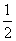 m﹣2.
m﹣2.
∵Rt△PCM与Rt△AOC相似,
∴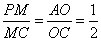 或
或 .
.
①若m<﹣2,则MC=4﹣m.
当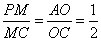 时,
时,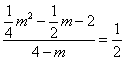 ,
,
解得m1=﹣4,m2=4(不合题意舍去),
此时点P的坐标为(﹣4,﹣4);
当 时,
时, ,
,
解得m1=﹣10,m2=4(不合题意舍去),
此时点P 的坐标为(﹣10,﹣28);
的坐标为(﹣10,﹣28);


科目:初中数学 来源: 题型:
已知二次函数y=x2+x+ ,当自变量x取m时对应的值小于0,当自变量x分别取m-1、m+1时对应的函数值为y1、y2,则y1、y2必须满足( )
A.y1>0、y2>0 B.y1<0、y2<0 C.y1<0、y2>0 D.y1>0、y2<0
查看答案和解析>>
科目:初中数学 来源: 题型:
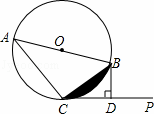
已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:△ACB∽△CDB;
(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
小明上周三在超市恰好用10元钱买了几袋牛奶,周日再去买时,恰遇超市搞优惠酬宾活动,同样的牛奶,每袋比周三便宜0.5元,结果小明只比上次多用了2元钱,却比上次多买了2袋牛奶.若设他上周三买了x袋牛奶,则根据题意列得方程为
查看答案和解析>>
科目:初中数学 来源: 题型:
天山旅行社为吸引游客组团去具有喀斯特地貌特征的黄果树风景区旅游,推出了如下收费标准(如图所示):

某单位组织员工去具有喀斯特地貌特征的黄果树风景区旅游, 共支付给旅行社旅游费用27000
共支付给旅行社旅游费用27000 元,请问该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游?
元,请问该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个口袋中有4个完全相同的小球,把它们分别标号为①,②,③,④,随机地摸出一个小球,记录后放回,再随机摸出一个小球,则两次摸出的小球的标号相同的概率是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
某电视台为了了解本地区电视节目的收视率情况,对部分观众开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了下面两幅不完整的统计图.根据要求回答下列问题:

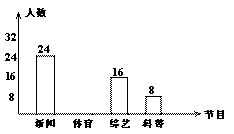
(1)本次问卷调查共调查了多少名观众?
(2)补全图1中的条形统计图;并求出图2中收看“综艺节目”的人数占调查总人数的百分比;
(3)求出图2中“科普节目”在扇形图中所对应的圆心角的度数;
(4) 现有喜欢“新闻节目”(记为A)、“体育节目”(记为B)、“综艺节目”(记为C)、“科普节目”(记为D)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用“列表法”或“画树形图”的方法求出恰好抽到喜欢“新闻节目”和“体育节目”两位观众的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com