
【题目】如图,直径为10的⊙O经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+48=0的两根.
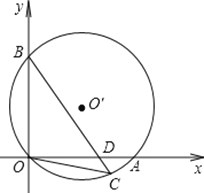
(1)求线段OA、OB的长;
(2)已知点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求C点的坐标;
(3)在⊙O上是否存在点P,使S△POD=S△ABD.若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)OA=8,OB=6;(2)C(4,-2);(3)不存在,理由见解析.
【解析】
(1)根据根与系数的关系写出OA+OB和OAOB的值.连接AB,根据90°的圆周角所对的弦是直径,再结合勾股定理列方程求解.
(2)若OC2=CDCB,则三角形OCB相似于三角形DCO,则∠COD=∠CBO.又∠COD=∠CBA,则∠CBO=∠CBA,所以点C是弧OA的中点.连接O′C,根据垂径定理的推论,得O′E⊥OA.再进一步根据垂径定理和勾股定理进行计算即可.
(3)首先求得直线BC的解析式,求得D的坐标,根据面积相等即可求得P的纵坐标,根据圆的直径即可作出判断.
解:(1)连接AB,∵∠BOA=90°,

∴AB为直径,根与系数关系得OA+OB=-k,OAOB=48;
根据勾股定理,得OA2+OB2=100,
即(OA+OB)2-2OAOB=100,
解得k2=196,∴k=±14(正值舍去).
则有方程x2-14x+48=0,x=6或8.
又OA>OB,
∴OA=8,OB=6.
(2)若OC2=CD×CB,则△OCB∽△DCO,
∴∠COD=∠CBO,
又∵∠COD=∠CBA,
∴∠CBO=∠CBA,
所以点C是弧OA的中点.
连接O′C交OA于点D,根据垂径定理的推论,得O′C⊥OA,
根据垂径定理,得OD=4,
根据勾股定理,得O′D=3,
∴CD=2,即C(4,-2).
(3)设直线BC的解析式是y=kx+b,把B(0,6),C(4,-2)代入
解得:K=-2,b=6
则直线BC的解析式是y=-2x+6,
令y=0,解得:x=3,
则OD=3,AD=8-3=5,
∴S△ABD=![]() ×5×6=15.
×5×6=15.
若S△ABD=S△OBD,P到x轴的距离是h,
则![]() ×3h=15,解得:h=10.
×3h=15,解得:h=10.
而⊙O′的直径是10,因而P不能在⊙O′上,
故P不存在.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
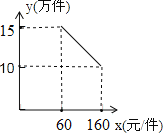
【题目】某公司2017年初刚成立时投资1000万元购买新生产线生产新产品,此外,生产每件该产品还需要成本40元.按规定,该产品售价不得低于60元/件且不超过160元/件,且每年售价确定以后不再变化,该产品的年销售量![]() (万件)与产品售价
(万件)与产品售价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求2017年该公司的最大利润?
(3)在2017年取得最大利润的前提下,2018年公司将重新确定产品售价,能否使两年共盈利达980万元.若能,求出2018年产品的售价;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,∠ABC=α,过点A作直线MN,使MN∥BC,点D在直线MN上,作射线BD,将射线BD绕点B顺时针旋转角α后交直线AC于点E.
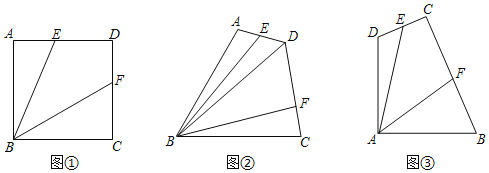
(1)如图①,当α=60°,且点D在射线AN上时,直接写出线段AB,AD,AE的数量关系.
(2)如图②,当α=45°,且点D在射线AN上时,直写出线段AB、AD、AE的数量关系,并说明理由.
(3)当α=30°时,若点D在射线AM上,∠ABE=15°,AD=![]() ﹣1,请直接写出线段AE的长度.
﹣1,请直接写出线段AE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国的数字支付正在引领未来世界的支付方式变革,中国消费者的移动支付比美国的移动支付要多出11倍,所以当我们展望数字钱包的未来时,中国是一个自然的起点.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,将各种支付方式调查人数组成一组数据,求这组数据的“中位数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求两人选同种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店在开学初用880元购进若干个学生专用科学计算器,按每个50元出售,很快就销售一空,据了解学生还急需3倍这种计算器,于是又用2580元购进所需计算器,由于量大每个进价比上次优惠1元,该店仍按每个50元销售,最后剩下4个按九折卖出.这笔生意该店共盈利( )元.
A.508 B.520 C.528 D.560
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E是正方形内都一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:(1)如图①,正方形ABCD中,点E,点F分别在边AD和边CD上,若正方形边长为4,DE+DF=4,则四边形BEDF的面积为 .
探究问题:(2)如图②,四边形ABCD,AB=BC=4,∠ABC=60°,∠ADC=120°,点E、F分别是边AD和边DC上的点,连接BE,BF,若ED+DF=3,BD=2![]() ,求四边形EBFD的面积;
,求四边形EBFD的面积;
解决问题:(3)某地质勘探队为了进行资源助测,建立了如图③所示的一个四边形野外勘查基地,基地相邻两侧边界DA、AB长度均为4km,∠DAB=90°,由于勘测需要及技术原因,主勘测仪C与基地边缘D、B夹角为90°(∠DCB=90°),在边界CD和边界BC上分别有两个辅助勘测仪E和F,辅助勘测仪E和F与主勘测仪C的距离之和始终等于4km(CE+CF=4).为了达到更好监测效果,需保证勘测区域(四边形EAFC)面积尽可能大.请问勘测区域面积有没有最大值,如果有求出最大值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,tan∠CAD=![]() ,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.

(1)求CD的长;
(2)若AF=2,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.
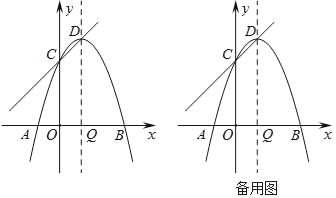
(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com