
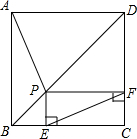
 如图,在正方形ABCD中,点P是对角线BD上的一点(不与端点重合),过P作PE⊥BC于E,PF⊥CD于F,连接AP,EF.
如图,在正方形ABCD中,点P是对角线BD上的一点(不与端点重合),过P作PE⊥BC于E,PF⊥CD于F,连接AP,EF.分析 (1)首先连接AC,PC,由四边形ABCD是正方形,可得BD垂直平分AC,即可证得AP=PC,又由PE⊥BC,PF⊥CD,证得四边形PECF是矩形,可判定EF=PC,继而证得结论;
(2)AP⊥EF.过点P作PN⊥AB,垂足为点N,延长AP,交EF于点M,利用全等三角形的判定定理可得△ANP≌△FPE(SSS),在△APN与△FPM中,根据三角形的内角和定理可得结论.
解答 (1)证明:连接AC,PC,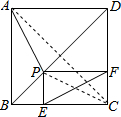
∵四边形ABCD是正方形,
∴BD垂直平分AC,∠BCD=90°,
∴AP=CP,
∵PE⊥BC,PF⊥CD,
∴∠PEC=∠PFC=90°,
∴四边形PECF是矩形,
∴PC=EF,
∴AP=EF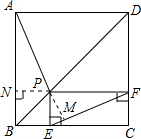
(2)解:AP⊥EF.
过点P作PN⊥AB,垂足为点N,延长AP,交EF于点M,
∵四边形ABCD是正方形,
∴∠ABP=∠CBD=45°,
∴△DFP为等腰直角三角形,
∴DF=PF,又AN=DF,
∴AN=FP,
又∵NP⊥AB,PE⊥BC,
∴四边形BNPE是正方形,
∴NP=EP,
又∵AP=PC,
四边形PECF为矩形,
∴EF=PC,
∴AP=EF,
在△ANP与△FPE中,
$\left\{\begin{array}{l}{AN=FP}\\{NP=EP}\\{AP=EF}\end{array}\right.$,
则△ANP≌△FPE(SSS),
∴∠NAP=∠PFE,
△APN与△FPM中,∠APN=∠FPM,∠NAP=∠PFM,
∴∠PMF=∠ANP=90°,
∴AP⊥EF.
点评 此题考查了正方形的性质、矩形的判定与性质以及线段垂直平分线的性质.注意准确作出辅助线是解此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 5$\sqrt{5}$ | C. | 8 | D. | 10$\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
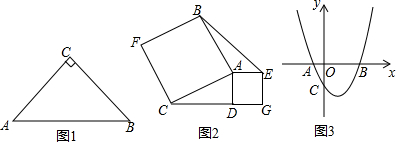
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
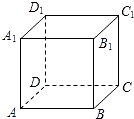 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )| A. | 0 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
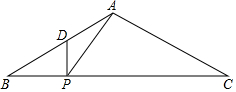 如图,在△ABC中,AB=AC=6,∠BAC=120°,点D是AB边上的点,$\frac{AD}{DB}$=$\frac{1}{2}$,点P为底边BC上的一动点,则△PDA周长的最小值为2$\sqrt{7}$+2.
如图,在△ABC中,AB=AC=6,∠BAC=120°,点D是AB边上的点,$\frac{AD}{DB}$=$\frac{1}{2}$,点P为底边BC上的一动点,则△PDA周长的最小值为2$\sqrt{7}$+2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “打开电视,正在播放新闻节目”是随机事件 | |
| B. | 为了解某种节能灯的使用寿命,选择全面调查 | |
| C. | 频数折线图能清楚的反映事物的变化情况,显示数据变化趋势 | |
| D. | 2016年我市有5.6万名初中毕业生参加升学考试,为了了解这5.6万名考生的数学成绩,从中抽取200名考生的数学成绩进行统计,在这个问题中样本是这200名考生的数学成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com