
ЁОЬтФПЁПЩЬГЁФГжжаТЩЬЦЗУПМўНјМлЪЧ40дЊЃЌдкЪдЯњЦкМфЗЂЯжЃЌЕБУПМўЩЬЦЗЪлМл50дЊЪБЃЌУПЬьПЩЯњЪл500МўЃЌЕБУПМўЩЬЦЗЪлМлИпгк50дЊЪБЃЌУПеЧМл5дЊЃЌШеЯњЪлСПОЭМѕЩй50МўЁЃОнДЫЙцТЩЃЌЧыЛиД№ЃК
(1)ЕБУПМўЩЬЦЗЪлМлЖЈЮЊ55дЊЪБЃЌУПЬьПЩЯњЪлЖрЩйМўЩЬЦЗ?ЩЬГЁЛёЕУЕФШегЏРћЪЧЖрЩй?
(2)дкЩЯЪіЬѕМўВЛБфЃЌЩЬЦЗЯњЪле§ГЃЕФЧщПіЯТЃЌУПМўЩЬЦЗЕФЯњЪлЖЈМлЮЊЖрЩйдЊЪБЃЌЩЬГЁШегЏРћПЩДяЕН8000дЊ?
ЁОД№АИЁПЃЈ1ЃЉ450ЃЌ6750ЃЈ2ЃЉ60дЊЛђ80дЊ
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгРћгУУПеЧМл5дЊЃЌШеЯњЪлСПОЭМѕЩй50МўЃЌНјЖјБэЪОГіУПЬьЕФЯњСПЃЌНјЖјБэЪОГіРћШѓЃЛ
ЃЈ2ЃЉЪзЯШБэЪОГіЯњСПгыУПМўЩЬЦЗРћШѓЕФГЫЛ§НјЖјЕУГізмРћШѓЮЊ8000дЊЃЌЕУГіЕШЪНЧѓГіД№АИЃЎ
(1)ЕБУПМўЩЬЦЗЪлМлЖЈЮЊ55дЊЪБЃЌ
УПЬьПЩЯњЪлЃК5005ЁС10=450(Мў)ЃЌ
ЩЬГЁЛёЕУЕФШегЏРћЪЧЃК450ЁС15=6750(дЊ)ЃЌ
Д№ЃКУПЬьПЩЯњЪл450МўЩЬЦЗЃЌЩЬГЁЛёЕУЕФШегЏРћЪЧ6750дЊЃЛ
(2)ЩшеЧМлxдЊЃЌдђИљОнЬтвтСаЗНГЬЕУЃК
(50010x)(50+x40)=8000ЃЌ
ећРэЕУГіЃКx![]() 40x+300=0,(x10)(x30)=0ЃЌ
40x+300=0,(x10)(x30)=0ЃЌ
НтЕУЃКx![]() =10 x
=10 x![]() =30ЃЌ
=30ЃЌ
ЙЪУПМўЩЬЦЗЕФЯњЪлЖЈМлЮЊЃК50+10=60(дЊ),30+50=80(дЊ)ЃЌ
Д№ЃКУПМўЩЬЦЗЕФЯњЪлЖЈМлЮЊ60дЊЛђ80дЊЪБЃЌЩЬГЁШегЏРћПЩДяЕН8000дЊЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНааЫФБпаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() ЁЂ
ЁЂ![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчгвЭМЃЌOЮЊдВзЖЕФЖЅЕуЃЌMЮЊЕзУцдВжмЩЯвЛЕуЃЌЕуPдкOMЩЯЃЌвЛжЛТьвЯДгЕуPГіЗЂШЦдВзЖВрУцХРааЛиЕНЕуPЪБЫљОЙ§ЕФзюЖЬТЗОЖЕФКлМЃШчЭМЃЎШєбиOMНЋдВзЖВрУцМєПЊВЂеЙЦНЃЌЫљЕУВрУцеЙПЊЭМЪЧЃЈЁЁЁЁЃЉ
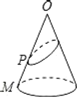
A.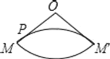 B.
B.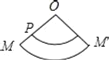
C.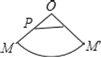 D.
D.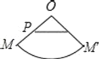
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЂХ ЮЪЬтЗЂЯж
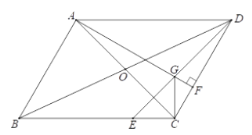
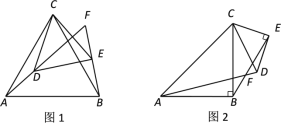
ЂХ ШчЭМ1ЃЌЁїABCКЭЁїCDEОљЮЊЕШБпШ§НЧаЮЃЌжБЯпADКЭжБЯпBEНЛгкЕуFЃЎ
ЬюПеЃКЂй![]() ЕФЖШЪ§ЪЧ________ЃЛЂкЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЮЊ________ЃЛ
ЕФЖШЪ§ЪЧ________ЃЛЂкЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЮЊ________ЃЛ
ЂЦ РрБШЬНОП
ШчЭМ2ЃЌЁїABCКЭЁїCDEОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжБЯпADКЭжБЯпBEНЛгкЕуFЃЎЧыХаЖЯ
ЃЌжБЯпADКЭжБЯпBEНЛгкЕуFЃЎЧыХаЖЯ![]() ЕФЖШЪ§МАЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЕФЖШЪ§МАЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЂЧ НтОіЮЪЬт
ШчЭМ3ЃЌдкЁїABCжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕуDдкABБпЩЯЃЌ
ЃЌЕуDдкABБпЩЯЃЌ![]() гкЕуEЃЌ
гкЕуEЃЌ![]() ЃЌНЋЁїADEШЦзХЕуAдкЦНУцФка§зЊЃЌЧыжБНгаДГіжБЯпDEОЙ§ЕуBЪБЃЌЕуCЕНжБЯпDEЕФОрРыЃЎ
ЃЌНЋЁїADEШЦзХЕуAдкЦНУцФка§зЊЃЌЧыжБНгаДГіжБЯпDEОЙ§ЕуBЪБЃЌЕуCЕНжБЯпDEЕФОрРыЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќМИФъЙКЮяЕФжЇИЖЗНЪНШевцдіЖрЃЌФГЪ§бЇаЫШЄаЁзщОЭДЫНјааСЫГщбљЕїВщЃЎЕїВщНсЙћЯдЪОЃЌжЇИЖЗНЪНгаЃКAЮЂаХЁЂBжЇИЖБІЁЂCЯжН№ЁЂDЦфЫћЃЌИУаЁзщЖдФГГЌЪавЛЬьФкЙКТђепЕФжЇИЖЗНЪННјааЕїВщЭГМЦЃЌЕУЕНШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ЧыФуИљОнЭГМЦЭМЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮвЛЙВЕїВщСЫЖрЩйУћЙКТђепЃП
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛдкЩШаЮЭГМЦЭМжаAжжжЇИЖЗНЪНЫљЖдгІЕФдВаФНЧЮЊЁЁ ЁЁЖШЃЎ
ЃЈ3ЃЉШєИУГЌЪаетвЛжмФкга1600УћЙКТђепЃЌЧыФуЙРМЦЪЙгУAКЭBСНжжжЇИЖЗНЪНЕФЙКТђепЙВгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАаЃдАЪжЛњЁБЯжЯѓдНРДдНЪмЕНЩчЛсЕФЙизЂЃЎЁАЮхвЛЁБЦкМфЃЌаЁМЧепСѕУњЫцЛњЕїВщСЫГЧЧјШєИЩУћбЇЩњКЭМвГЄЖджабЇЩњДјЪжЛњЯжЯѓЕФПДЗЈЃЌЭГМЦећРэВЂжЦзїСЫШчЯТЕФЭГМЦЭМЃК
ЃЈ1ЃЉЧѓетДЮЕїВщЕФМвГЄШЫЪ§ЃЌВЂВЙШЋЭМЂйЃЛ
ЃЈ2ЃЉЧѓЭМЂкжаБэЪОМвГЄЁАдоГЩЁБЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчЙћИУЪага8ЭђУћГѕжаЩњЃЌГжЁАЮоЫљЮНЁБЬЌЖШЕФбЇЩњДѓдМгаЖрЩйШЫЃП
ЃЈ4ЃЉДгетДЮНгЪмЕїВщЕФМвГЄгыбЇЩњжаЫцЛњГщВщвЛИіЃЌЧЁКУЪЧЁАЮоЫљЮНЁБЬЌЖШЕФИХТЪЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁб![]() ЕФжБОЖЃЌЙ§ЕуAзїЁб
ЕФжБОЖЃЌЙ§ЕуAзїЁб![]() ЕФЧаЯпВЂдкЦфЩЯШЁвЛЕуCЃЌСЌНгOCНЛЁб
ЕФЧаЯпВЂдкЦфЩЯШЁвЛЕуCЃЌСЌНгOCНЛЁб![]() гкЕуDЃЌBDЕФбгГЄЯпНЛACгкEЃЌСЌНгAD.
гкЕуDЃЌBDЕФбгГЄЯпНЛACгкEЃЌСЌНгAD.
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєAB=2ЃЌ![]() ЃЌЧѓAEЕФГЄ.
ЃЌЧѓAEЕФГЄ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчзгГЇЩЬЭЖВњвЛжжаТаЭЕчзгВњЦЗЃЌУПМўжЦдьГЩБОЮЊ18дЊЃЌЪдЯњЙ§ГЬжаЗЂЯжЃЌУПдТЯњЪлСП![]() ЃЈЭђМўЃЉгыЯњЪлЕЅМл
ЃЈЭђМўЃЉгыЯњЪлЕЅМл![]() ЃЈдЊЃЉжЎМфЕФЙиЯЕПЩвдНќЫЦЕиПДзївЛДЮКЏЪ§
ЃЈдЊЃЉжЎМфЕФЙиЯЕПЩвдНќЫЦЕиПДзївЛДЮКЏЪ§![]() ЃЈРћШѓ=ЪлМлЉжЦдьГЩБОЃЉ
ЃЈРћШѓ=ЪлМлЉжЦдьГЩБОЃЉ
ЃЈ1ЃЉаДГіУПдТЕФРћШѓ![]() ЃЈЭђдЊЃЉгыЯњЪлЕЅМл
ЃЈЭђдЊЃЉгыЯњЪлЕЅМл![]() ЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉИљОнЯрЙиВПУХЙцЖЈЃЌетжжЕчзгВњЦЗЕФЯњЪлЕЅМлВЛФмИпгк40дЊЃЌШчЙћГЇЩЬУПдТЕФжЦдьГЩБОВЛГЌЙ§540ЭђдЊЃЌФЧУДЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌГЇЩЬУПдТЛёЕУЕФРћШѓзюДѓЃПзюДѓРћШѓЮЊЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
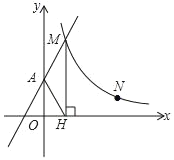
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃН2x+2гыyжсНЛгкAЕуЃЌгыЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуMЃЌЙ§MзїMHЁЭxжсгкЕуHЃЌЧвtanЁЯAHOЃН2ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуMЃЌЙ§MзїMHЁЭxжсгкЕуHЃЌЧвtanЁЯAHOЃН2ЃЎ
ЃЈ1ЃЉЧѓHЕуЕФзјБъМАkЕФжЕЃЛ
ЃЈ2ЃЉЕуPдкyжсЩЯЃЌЪЙЁїAMPЪЧвдAMЮЊбќЕФЕШбќШ§НЧаЮЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФPЕузјБъЃЛ
ЃЈ3ЃЉЕуNЃЈaЃЌ1ЃЉЪЧЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЭМЯѓЩЯЕФЕуЃЌЕуQЃЈmЃЌ0ЃЉЪЧxжсЩЯЕФЖЏЕуЃЌЕБЁїMNQЕФУцЛ§ЮЊ3ЪБЃЌЧыЧѓГіЫљгаТњзуЬѕМўЕФmЕФжЕЃЎ
ЃЈxЃО0ЃЉЭМЯѓЩЯЕФЕуЃЌЕуQЃЈmЃЌ0ЃЉЪЧxжсЩЯЕФЖЏЕуЃЌЕБЁїMNQЕФУцЛ§ЮЊ3ЪБЃЌЧыЧѓГіЫљгаТњзуЬѕМўЕФmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com