
(1)åáÑêüôêÅáÖàïȤ
¥¡¡—ý£çàÆÖêÐçáò»üÁ°ùȘ£»çáñ«¤éÆ衤طò»çá¡—ò»ƒ—Ñ´ÈÛâ»àÓȘ¢¥ýÕǺò»ò§(xÈÙ1)(xÈÙ2)çáøçȤ
çÝxÈ¥1ȘxÈÙ1È¥0ȘxÈÙ2È¥0Ș
ùªØå(xÈÙ1)(xÈÙ2)ȃ0È£
çÝ1È¥xÈ¥2òÝȘxÈÙ1ȃ0ȘxÈÙ2È¥0Ș
ùªØå(xÈÙ1)(xÈÙ2)È¥0È£
çÝxȃ2òÝȘxÈÙ1ȃ0ȘxÈÙ2ȃ0Ș
ùªØå(xÈÙ1)(xÈÙ2)ȃ0ÈÛ
ùªØåçÝxÈ¥1£·xȃ2òÝȘ(xÈÙ1)(xÈÙ2)ȃ0È£
çÝ1È¥xÈ¥2òÝȘ(xÈÙ1)(xÈÙ2)È¥0ÈÛ
(2)äŸÅÇüôÝÚȤ(ÆûÀ¯È¨ÀÝ£·À¯ÈÙÀÝäŸàŠ¢í¡þÇÎ)
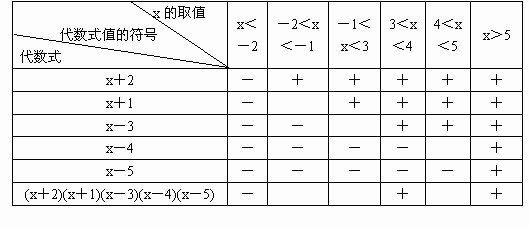
(3)¡ªƒïØåèüäŸÝÚȘÅÇ°—çÝx_______òÝȘ(xȨ2)(xȨ1)(xÈÙ3)(xÈÙ4)(xÈÙ5)È¥0È£úŠáÐåùÆûùªñÂüøçá¿ÌôèÅÇ°—çÝx_______òÝȘ(xÈÙ8)(xÈÙ9)(xÈÙ10)(xÈÙ11)ȃ0ÈÛ
|
ÀÀÀÀÇÞ¯¡È¤ (2)ØâÇöäŸàŠÈÙ,ÈÙ,Ȩ,Ȩ,ÈÙ,ÈÙÀÀÀÀ (3)ØâÇöäŸÅÇxÈ¥ÈÙ2£·ÈÙ1È¥xÈ¥3£·4È¥xÈ¥5,xÈ¥8£·9È¥xÈ¥10£·xȃ11ÈÛÀÀÀÀóòö—Ȥ¥¡¡—ý£çàÆÖ 0çáò»£·ò§üÁ°ùȘ£»çáñ«¤éÆ衤طò»(ò§)çá¡—ò»ƒ—Ñ´ÈÛë´¿»åáÑê(1)çûç§ó¶òƒÈ˜àñÑ´xȨ1ȘxÈÙ3ȘxÈÙ4ȘxÈÙ5¥¯(xȨ2)(xȨ1)(xÈÙ3)(xÈÙ4)(xÈÙ5)çáí»¡¤úÕ¢—ȘƊxçáàÀøçñÑöÏÆÅ¿ÄȘ(3)¢èØåøݧÆåáÑêÝÚ¡þäŸÅÇÈÛ |


 äšäšü·èüأ݃¤ûƒÚüçêÅÇÞ¯¡
äšäšü·èüأ݃¤ûƒÚüçêÅÇÞ¯¡ ÅÀîÏèº10ñøøÆÆÎÆûäãüçêÅÇÞ¯¡
ÅÀîÏèº10ñøøÆÆÎÆûäãüçêÅÇÞ¯¡
| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
| 1 |
| 1Àê2 |
| 1 |
| 2 |
| 1 |
| 2Àê3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3Àê4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9Àê10 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 1Àê2 |
| 1 |
| 2Àê3 |
| 1 |
| 9Àê10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 10 |
| 9 |
| 10 |
| 1 |
| 1Àê2 |
| 1 |
| 2Àê3 |
| 1 |
| 2006Àê2007 |
| 1 |
| 1Àê3 |
| 1 |
| 3Àê5 |
| 1 |
| 5Àê7 |
| 1 |
| 2005Àê2007 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
| 1 |
| 1Àê2 |
| 1 |
| 2 |
| 1 |
| 2Àê3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3Àê4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4Àê5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| nÀê(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2007)(b+2007) |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤåáÑêâÚ§ã
| xȥ-2 | -2ȥxȥ-1 | -1ȥxȥ3 | xȃ3 | |
| x+2 | - | + | + | + |
| x+1 | - | - | + | + |
| x-3 | - | - | - | + |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤåáÑêâÚ§ã
| 206 |
| 299 |
| 206 |
| 299 |
| 206 |
| 299 |
| 206 |
(
| ||||
|
| 206-142 | ||
|
| 10 | ||
|
| 299 |
(
| ||||
|
| 299-172 | ||
|
| 10 | ||
|
| 299 |
| 206 |
| 299 |
| 206 |
| 10 | ||
|
| 10 | ||
|
| a+5 |
| a+2 |
| a+3 |
| a |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤåáÑêâÚ§ã
| 199009922 |
| 199009912+199009932-2 |
| x2 |
| (x-1)2+(x+1)2-2 |
| x2 |
| 2x2 |
| 1 |
| 2 |
| 1 |
| 2006 |
| 2008 |
| 20052-1 |
| 20042 |
| 20072-1 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¯ìÑàøôÅé - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com