
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2.
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2. 分析 根据图象的旋转变化规律以及二次函数的平移规律得出平移后解析式,进而求出m的值.
解答 解:∵一段抛物线:y=-x(x-3)(0≤x≤3),
∴图象与x轴交点坐标为:(0,0),(3,0),
∵将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.
∴C13的解析式与x轴的交点坐标为(36,0),(39,0),且图象在x轴上方,
∴C13的解析式为:y13=-(x-36)(x-39),
当x=37时,y=-(38-36)×(38-39)=2,
∴m=2.
故答案为:2.
点评 此题主要考查了二次函数的平移规律,根据已知得出二次函数旋转后解析式是解题关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
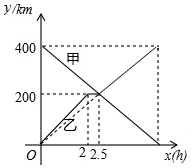 甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km
甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
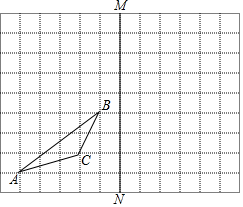 如图,已知三角形ABC和直线MN,且三角形ABC的顶点在网格的交点上.
如图,已知三角形ABC和直线MN,且三角形ABC的顶点在网格的交点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
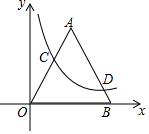 已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点C和点D,则k的值为( )
已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点C和点D,则k的值为( )| A. | $\frac{81\sqrt{3}}{25}$ | B. | $\frac{81\sqrt{3}}{16}$ | C. | $\frac{81\sqrt{3}}{5}$ | D. | $\frac{81\sqrt{3}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
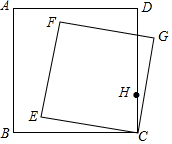 如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{2}}{5}$ | C. | $\frac{\sqrt{2}}{7}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com