
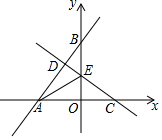
 如图,直线l1:y=$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:y=-$\frac{3}{4}$x+b经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
如图,直线l1:y=$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:y=-$\frac{3}{4}$x+b经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.分析 (1)①由点C的坐标,利用待定系数法即可求出b值,此题得解;
②利用一次函数图象上点的坐标特征可求出点A、E的坐标,利用勾股定理以及两点间的距离即可求出AC=AB,由正切的定义即可得出∠ABO=∠ACD,结合公共角即可利用全等三角形的判定定理ASA证出△ABO≌△ACD,从而得出AO=AD、∠ADC=∠AOB=90°,再利用全等直角三角形的判定定理HL即可证出Rt△ADE≌Rt△AOE,根据全等三角形的性质可找出∠DAE=∠OAE,由此即可证出AE平分∠BAC;
(2)△ACE是以CE为一腰的等腰三角形分两种情况:①CE=AE时,利用等腰三角形的性质结合点A的坐标即可得出点C的坐标;②当CA=CE时,设点C(m,0)(m>0),则OC=m,OE=$\frac{3}{4}$OC=$\frac{3}{4}$m,CA=m+2,利用勾股定理求出CE,由CA=CE即可得出关于m的一元一次方程,解之即可得出点C的坐标.综上即可得出结论.
解答 解:(1)①将C(2,0)代入y=-$\frac{3}{4}$x+b,
0=-$\frac{3}{4}$×2+b,解得:b=$\frac{3}{2}$,
∴直线l2的函数表达式为y=-$\frac{3}{4}$x+$\frac{3}{2}$.
②证明:当y=$\frac{4}{3}$x+4=0时,x=-3,
∴点A(-3,0),
∴tan∠ABO=$\frac{OA}{OB}$=$\frac{3}{4}$,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,AC=2-(-3)=5=AB.
∵当x=0时,y=-$\frac{3}{4}$x+$\frac{3}{2}$=$\frac{3}{2}$,
∴tan∠AOD=$\frac{OE}{OC}$=$\frac{3}{4}$,
∴∠ABO=∠ACD.
在△ABO和△ACD中,$\left\{\begin{array}{l}{∠ABO=∠ACD}\\{AB=AC}\\{∠BAO=∠CAD}\end{array}\right.$,
∴△ABO≌△ACD(ASA),
∴AO=AD,∠ADC=∠AOB=90°.
在Rt△ADE和Rt△AOE中,$\left\{\begin{array}{l}{AD=AO}\\{AE=AE}\end{array}\right.$,
∴Rt△ADE≌Rt△AOE(HL),
∴∠DAE=∠OAE,
∴AE平分∠BAC.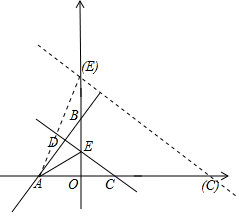
(2)△ACE是以CE为一腰的等腰三角形分两种情况:
①当AE=CE时,∵EO⊥AC,
∴OC=OA,
∴点C(3,0);
②当CA=CE时,设点C(m,0)(m>0),则OC=m,OE=$\frac{3}{4}$OC=$\frac{3}{4}$m,CA=m+2,
∴CE=$\sqrt{O{E}^{2}+O{C}^{2}}$=$\frac{5}{4}$m,
∴m+2=$\frac{5}{4}$m,
解得:m=8,
∴点C(8,0).
综上所述:存在点C,使△ACE是以CE为一腰的等腰三角形,点C的坐标为(3,0)或(8,0).
点评 本题考查了待定系数法求一次函数解析式、全等三角形的判定与性质、勾股定理、两点间的距离以及等腰三角形的性质,解题的关键是:(1)①由点C的坐标利用待定系数法求出b值;②利用全等三角形的判定与性质证出∠DAE=∠OAE;(2)分AE=CE和CA=CE两种情况考虑.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:解答题
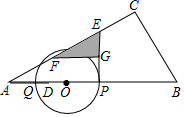 如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC-CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.
如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC-CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y≤-2 | B. | y≥4 | C. | y2-2y-8≥0 | D. | 一切实数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
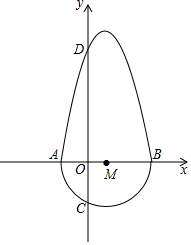 定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为3.
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
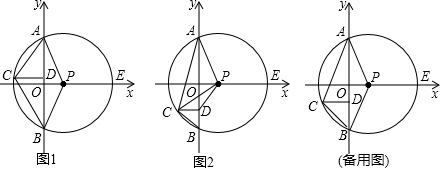
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com