
分析 (1)把抛物线解析式写成顶点式,可用a分别表示出b和c,可得到b和c之间的关系式;
(2)①由条件可知△ODE和△ODF同底,且高的比为E、F两点的横坐标之比,可求得△ODE和△ODF的面积之间的关系,可求得答案;
②可设出E点坐标为(m,m+4),表示出F点的坐标,由条件可证明△EPM∽△PFN,根据相似三角形的性质可得到关于m的方程,可求得m,可求得E、F点的坐标,把F点坐标代入抛物线解析式可求得a的值,再把E点坐标代入验证即可.
解答  解:(1)∵抛物线顶点坐标为(2,4),
解:(1)∵抛物线顶点坐标为(2,4),
∴抛物线解析式为y=a(x-2)2+4=ax2-4ax+4a+4,
∴b=-4a,c=4a+4,
∴b+c=4;
(2)①由题意可知△ODE和△ODF的底边DE、DF边上的高相同,
∴S△ODE:S△ODF=DE:DF=x1:x2=1:6,
∴S△ODE:S△OEF=1:5;
②如图,分别过E、F作x轴的垂线,垂足分别为G、H,交直线DP于点M、N,
∵直线y=x+4,
∴设点E坐标为(m,m+4),则点F的坐标为(6m,6m+4),
∴EM=EG-MG=m+4-4=m,FN=FH-NH=6m+4-4=6m,PM=PD-MD=2-m,PN=DN-PD=6m-2,
∵∠EPF=90°,
∴∠EPM+∠FPN=90°,且∠FPN+∠PFN=90°,
∴∠EPM=∠PFN,
∴△EPM∽△PEN,
∴$\frac{EM}{PN}$=$\frac{PM}{FN}$,即$\frac{m}{6m-2}$=$\frac{2-m}{6m}$,
整理可得6m2+7m+2=0,解得m=$\frac{1}{2}$或m=$\frac{2}{3}$,
当m=$\frac{1}{2}$时,点E($\frac{1}{2}$,$\frac{9}{2}$),F(3,7),把F点坐标代入抛物线解析式可得a+4=7,解得a=3,
∴抛物线解析式为y=3(x-2)2+4,当x=$\frac{1}{2}$时,代入可求得y=$\frac{43}{4}$≠$\frac{9}{2}$,即点E不在该抛物线图象上,不符合题意,
当m=$\frac{2}{3}$时,点E($\frac{2}{3}$,4$\frac{2}{3}$),F(4,8),把F点坐标代入抛物线解析式可求得a=1,
∴抛物线解析式为y=(x-2)2+4,当x=$\frac{2}{3}$时,代入可求得y=$\frac{52}{9}$≠4$\frac{2}{3}$,即点E不在抛物线图象上,不符合题意,
综上可知不存在满足条件的a的值.
点评 本题主要考查二次函数的综合应用,涉及知识点有待定系数法、三角形的面积、相似三角形的判定和性质、一元二次方程等.在(1)中写出抛物线线的顶点式是解题的关键,在(2)①中利用同高三角形的面积比为底的比是解题的关键,在②中利用相似三角形性质求得E、F的坐标是解题的关键,注意代入验证.本题考查知识点较多,综合性较强,难度较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
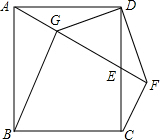 如图,已知在正方形ABCD中,点E在CD边长,过C点作AE的垂线交于点F,联结DF,过点D作DF的垂线交A于点G,联结BG.
如图,已知在正方形ABCD中,点E在CD边长,过C点作AE的垂线交于点F,联结DF,过点D作DF的垂线交A于点G,联结BG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 需要女生 | 需要男生 | |
| 甲种活动 | 7人 | 4人 |
| 乙种活动 | 3人 | 10人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )| A. | 甲比乙先到达终点 | |
| B. | 甲比乙多走了200米 | |
| C. | 乙比甲少用了0.2分钟 | |
| D. | 比赛中两人从出发到2.2分钟时间段,乙的速度比甲的速度快 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com