
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏyΘΫ![]() x2+bx+c”κ÷±œΏyΘΫ
x2+bx+c”κ÷±œΏyΘΫ![]() x+3Ζ÷±πœύΫΜ”ΎAΘ§BΝΫΒψΘ§«“¥Υ≈ΉΈοœΏ”κx÷αΒΡ“ΜΗωΫΜΒψΈΣCΘ§Ν§Ϋ”ACΘ§BCΘ°“―÷ΣAΘ®0Θ§3Θ©Θ§CΘ®©¹3Θ§0Θ©Θ°
x+3Ζ÷±πœύΫΜ”ΎAΘ§BΝΫΒψΘ§«“¥Υ≈ΉΈοœΏ”κx÷αΒΡ“ΜΗωΫΜΒψΈΣCΘ§Ν§Ϋ”ACΘ§BCΘ°“―÷ΣAΘ®0Θ§3Θ©Θ§CΘ®©¹3Θ§0Θ©Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
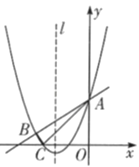
Θ®2Θ©‘Ύ≈ΉΈοœΏΕ‘≥Τ÷αl…œ’““ΜΒψMΘ§ Ι|MB©¹MC|ΒΡ÷ΒΉν¥σΘ§≤Δ«σ≥ω’βΗωΉν¥σ÷ΒΘΜ
Θ®3Θ©ΒψPΈΣy÷α”“≤ύ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§Ν§Ϋ”PAΘ§ΙΐΒψPΉςPQΓΆPAΫΜy÷α”ΎΒψQΘ§Έ ΘΚ «Ζώ¥φ‘ΎΒψP ΙΒΟ“‘AΘ§PΘ§QΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫ![]() x2+
x2+![]() x+3ΘΜΘ®2Θ©|MB©¹MC|»ΓΉν¥σ÷ΒΈΣ
x+3ΘΜΘ®2Θ©|MB©¹MC|»ΓΉν¥σ÷ΒΈΣ![]() ΘΜΘ®3Θ©¥φ‘ΎΘ§ΒψPΘ®1Θ§6Θ©Θ°
ΘΜΘ®3Θ©¥φ‘ΎΘ§ΒψPΘ®1Θ§6Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌΫΪAΘ®0Θ§3Θ©Θ§CΘ®-3Θ§0Θ©¥ζ»κy=![]() x2+bx+cΘ§Φ¥Ω…«σΫβΘΜ
x2+bx+cΘ§Φ¥Ω…«σΫβΘΜ
Θ®2Θ©Ζ÷Β±ΒψBΓΔCΓΔM»ΐΒψ≤ΜΙ≤œΏ ±ΓΔΒ±ΒψBΓΔCΓΔM»ΐΒψΙ≤œΏ ±Θ§ΝΫ÷÷«ιΩωΖ÷±π«σΫβΦ¥Ω…ΘΜ
Θ®3Θ©Ζ÷Β±![]() ±ΓΔΒ±
±ΓΔΒ±![]() ±ΝΫ÷÷«ιΩωΘ§Ζ÷±π«σΫβΦ¥Ω…Θ°
±ΝΫ÷÷«ιΩωΘ§Ζ÷±π«σΫβΦ¥Ω…Θ°
Θ®1Θ©ΫΪAΘ®0Θ§3Θ©Θ§CΘ®©¹3Θ§0Θ©¥ζ»κyΘΫ![]() x2+bx+cΘ§
x2+bx+cȧ
ΒΟ Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω Ϋ «yΘΫ![]() x2+
x2+![]() x+3ΘΜ
x+3ΘΜ
Θ®2Θ©ΫΪ÷±œΏyΘΫ![]() x+3±μ¥ο Ϋ”κΕΰ¥ΈΚ· ΐ±μ¥ο ΫΝΣΝΔ≤ΔΫβΒΟΘΚxΘΫ0Μρ©¹4Θ§
x+3±μ¥ο Ϋ”κΕΰ¥ΈΚ· ΐ±μ¥ο ΫΝΣΝΔ≤ΔΫβΒΟΘΚxΘΫ0Μρ©¹4Θ§
ΓΏA Θ®0Θ§3Θ©Θ§
ΓύBΘ®©¹4Θ§1Θ©
ΔΌΒ±ΒψBΓΔCΓΔM»ΐΒψ≤ΜΙ≤œΏ ±Θ§
|MB©¹MC|ΘΦBCΘ§
ΔΎΒ±ΒψBΓΔCΓΔM»ΐΒψΙ≤œΏ ±Θ§
|MB©¹MC|ΘΫBCΘ§
ΓύΒ±ΒψΓΔCΓΔM»ΐΒψΙ≤œΏ ±Θ§|MB©¹MC|»ΓΉν¥σ÷ΒΘ§Φ¥ΈΣBCΒΡ≥ΛΘ§
ΙΐΒψBΉςx÷α”ΎΒψEΘ§

‘ΎRtΓςBEC÷–Θ§”…Ι¥Ι…Ε®άμΒΟBCΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
Γύ|MB©¹MC|»ΓΉν¥σ÷ΒΈΣ![]() ΘΜ
ΘΜ
Θ®3Θ©¥φ‘ΎΒψP ΙΒΟ“‘AΓΔPΓΔQΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ°
…ηΒψPΉχ±ξΈΣΘ®xΘ§![]() x2+
x2+![]() x+3Θ©Θ®xΘΨ0Θ©
x+3Θ©Θ®xΘΨ0Θ©
‘ΎRtΓςBEC÷–Θ§
ΓΏBEΘΫCEΘΫ1Θ§
ΓύΓœBCEΘΫ45ΓψΘ§
‘ΎRtΓςACO÷–Θ§
ΓΏAOΘΫCOΘΫ3Θ§
ΓύΓœACOΘΫ45ΓψΘ§
ΓύΓœACBΘΫ180Γψ©¹450©¹450ΘΫ900Θ§ACΘΫ3![]() Θ§
Θ§
ΙΐΒψPΉςPQΓΆPA”ΎΒψPΘ§‘ρΓœAPQΘΫ90ΓψΘ§ΙΐΒψPΉςPQΓΆy÷α”ΎΒψGΘ§

ΓΏΓœPQAΘΫΓœAPQΘΫ90Γψ
ΓœPAGΘΫΓœQAPΘ§
ΓύΓςPGAΓΉΓςQPA
ΓΏΓœPGAΘΫΓœACBΘΫ90Γψ
ΓύΔΌΒ±![]() ±Θ§
±Θ§
ΓςPAGΓΉΓςBACΘ§
Γύ Θ§
Θ§
ΫβΒΟx1ΘΫ1Θ§x2ΘΫ0Θ§Θ®…α»ΞΘ©
ΓύΒψPΒΡΉίΉχ±ξΈΣ![]() ΓΝ12+
ΓΝ12+![]() ΓΝ1+3ΘΫ6Θ§
ΓΝ1+3ΘΫ6Θ§
ΓύΒψPΈΣΘ®1Θ§6Θ©ΘΜ
ΔΎΒ±![]() ±Θ§
±Θ§
ΓςPAGΓΉΓςABCΘ§
Γύ Θ§
Θ§
ΫβΒΟx1ΘΫ©¹![]() Θ®…α»ΞΘ©Θ§x2ΘΫ0Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§x2ΘΫ0Θ®…α»ΞΘ©Θ§
Γύ¥Υ ±ΈόΖϊΚœΧθΦΰΒΡΒψP
Ήέ…œΥυ ωΘ§¥φ‘ΎΒψPΘ®1Θ§6Θ©Θ°


 ΩΈΩΈΝΖΫ≠Υ’œΒΝ–¥πΑΗ
ΩΈΩΈΝΖΫ≠Υ’œΒΝ–¥πΑΗ Οϊ≈Τ÷–―ßΩΈ ±Ής“ΒœΒΝ–¥πΑΗ
Οϊ≈Τ÷–―ßΩΈ ±Ής“ΒœΒΝ–¥πΑΗ ΟςΧλΫΧ”ΐΩΈ ±ΧΊ―ΒœΒΝ–¥πΑΗ
ΟςΧλΫΧ”ΐΩΈ ±ΧΊ―ΒœΒΝ–¥πΑΗ ’ψΫ≠–¬ΩΈ≥Χ»ΐΈ§ΡΩ±ξ≤βΤάΩΈ ±ΧΊ―ΒœΒΝ–¥πΑΗ
’ψΫ≠–¬ΩΈ≥Χ»ΐΈ§ΡΩ±ξ≤βΤάΩΈ ±ΧΊ―ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
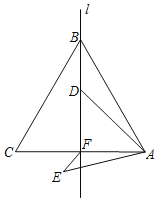
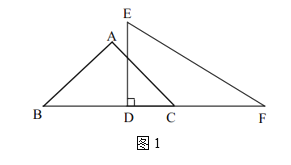
ΓΨΧβΡΩΓΩ»γΆΦΘ§Β»±Ώ»ΐΫ«–ΈΓςABCΒΡ±Ώ≥ΛΈΣ6Θ§l «AC±Ώ…œΒΡΗΏBFΥυ‘ΎΒΡ÷±œΏΘ§ΒψDΈΣ÷±œΏl…œΒΡ“ΜΕ·ΒψΘ§Ν§Ϋ”ADΘ§≤ΔΫΪAD»ΤΒψAΡφ ±’κ–ΐΉΣ60Γψ÷ΝAEΘ§Ν§Ϋ”EFΘ§‘ρEFΒΡΉν–Γ÷ΒΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
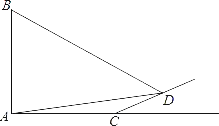
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤλΗΥABΒΡΕΞΕΥB‘ΎœΠ―τΒΡ”ύΜ‘œ¬¬δ‘Ύ“ΜΗω–±Τ¬…œΒΡΒψD¥ΠΘ§Ρ≥–Θ ΐ―ßΩΈΆβ–Υ»Λ–ΓΉιΒΡΆ§―ß’ΐ‘Ύ≤βΝΩΤλΗΥΒΡΗΏΕ»Θ§‘ΎΤλΗΥΒΡΒΉ≤ΩA¥Π≤βΒΟΒψDΒΡ―ωΫ«ΈΣ15ΓψΘ§ACΘΫ10ΟΉΘ§”÷≤βΒΟΓœBDAΘΫ45ΓψΘ°“―÷Σ–±Τ¬CDΒΡΤ¬Ε»ΈΣiΘΫ1ΘΚ![]() Θ§«σΤλΗΥABΒΡΗΏΕ»Θ®
Θ§«σΤλΗΥABΒΡΗΏΕ»Θ®![]() Θ§ΫαΙϊΨΪ»ΖΒΫΗωΈΜΘ©Θ°
Θ§ΫαΙϊΨΪ»ΖΒΫΗωΈΜΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΑύΈΣ≤ΈΦ”―ß–ΘΒΡ¥σΩΈΦδΜνΕ·±»»ϋΘ§ΉΦ±ΗΙΚΫχ“Μ≈ζΧχ…ΰΘ§“―÷Σ2Ηυ![]() –ΆΧχ…ΰΚΆ1Ηυ
–ΆΧχ…ΰΚΆ1Ηυ![]() –ΆΧχ…ΰΙ≤–η56‘ΣΘ§1Ηυ
–ΆΧχ…ΰΙ≤–η56‘ΣΘ§1Ηυ![]() –ΆΧχ…ΰΚΆ2Ηυ
–ΆΧχ…ΰΚΆ2Ηυ![]() –ΆΧχ…ΰΙ≤–η82‘ΣΘ°
–ΆΧχ…ΰΙ≤–η82‘ΣΘ°
Θ®1Θ©«σ“ΜΗυ![]() –ΆΧχ…ΰΚΆ“ΜΗυ
–ΆΧχ…ΰΚΆ“ΜΗυ![]() –ΆΧχ…ΰΒΡ έΦέΗς «Εύ…Ό‘ΣΘΩ
–ΆΧχ…ΰΒΡ έΦέΗς «Εύ…Ό‘ΣΘΩ
Θ®2Θ©―ß–ΘΉΦ±ΗΙΚΫχ’βΝΫ÷÷–ΆΚ≈ΒΡΧχ…ΰΙ≤50ΗυΘ§≤Δ«“![]() –ΆΧχ…ΰΒΡ ΐΝΩ≤ΜΕύ”Ύ
–ΆΧχ…ΰΒΡ ΐΝΩ≤ΜΕύ”Ύ![]() –ΆΧχ…ΰ ΐΝΩΒΡ3±ΕΘ§«κ…ηΦΤ≥ωΉν Γ«°ΒΡΙΚ¬ρΖΫΑΗΘ§≤ΔΥΒΟςάμ”…Θ°
–ΆΧχ…ΰ ΐΝΩΒΡ3±ΕΘ§«κ…ηΦΤ≥ωΉν Γ«°ΒΡΙΚ¬ρΖΫΑΗΘ§≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΤκΤκΙΰΕϊ –ΫΧ”ΐΨ÷œκ÷ΣΒάΡ≥–Θ―ß…ζΕ‘‘ζΝζΉ‘»Μ±ΘΜΛ«χΒΡΝΥΫβ≥ΧΕ»Θ§‘ΎΗΟ–ΘΥφΜζ≥ι»ΓΝΥ≤ΩΖ÷―ß…ζΫχ––Έ ΨμΘ§Έ Ψμ”–“‘œ¬ΥΡΗω―ΓœνΘΚAΘ° °Ζ÷ΝΥΫβΘΜBΘ°ΝΥΫβΫœΕύΘΚCΘ°ΝΥΫβΫœ…ΌΘΚDΘ°≤ΜΝΥΫβΘ®“Σ«σΘΚΟΩΟϊ±ΜΒς≤ιΒΡ―ß…ζ±Ί―Γ«“÷ΜΡή―Γ‘ώ“ΜœνΘ©Θ°œ÷ΫΪΒς≤ιΒΡΫαΙϊΜφ÷Τ≥…ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°«κΗυΨίΝΫΖυΆ≥ΦΤΆΦ÷–ΒΡ–≈œΔΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©±Ψ¥Έ±Μ≥ι»ΓΒΡ―ß…ζΙ≤”–_______ΟϊΘΜ
Θ®2Θ©«κ≤Ι»ΪΧθ–ΈΆΦΘΜ
Θ®3Θ©…»–ΈΆΦ÷–ΒΡ―ΓœνΓΑCΘ°ΝΥΫβΫœ…ΌΓ±≤ΩΖ÷Υυ’Φ…»–ΈΒΡ‘≤–ΡΫ«ΒΡ¥σ–ΓΈΣ_______ΓψΘΜ
Θ®4Θ©»τΗΟ–ΘΙ≤”–![]() Οϊ―ß…ζΘ§«κΡψΗυΨί…œ ωΒς≤ιΫαΙϊΙάΦΤΗΟ–ΘΕ‘”Ύ‘ζΝζΉ‘»Μ±ΘΜΛ«χΓΑ °Ζ÷ΝΥΫβΓ±ΚΆΓΑΝΥΫβΫœΕύΓ±ΒΡ―ß…ζΙ≤”–Εύ…ΌΟϊΘΩ
Οϊ―ß…ζΘ§«κΡψΗυΨί…œ ωΒς≤ιΫαΙϊΙάΦΤΗΟ–ΘΕ‘”Ύ‘ζΝζΉ‘»Μ±ΘΜΛ«χΓΑ °Ζ÷ΝΥΫβΓ±ΚΆΓΑΝΥΫβΫœΕύΓ±ΒΡ―ß…ζΙ≤”–Εύ…ΌΟϊΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΑκΨΕΈΣ1ΒΡΓ―O”κx÷α’ΐΑκ÷αΚΆy÷α’ΐΑκ÷αΖ÷±πΫΜ”ΎAΘ§BΝΫΒψΘ§÷±œΏlΘΚyΘΫkx+2Θ®kΘΦ0Θ©”κx÷αΚΆy÷αΖ÷±πΫΜ”ΎPΘ§MΝΫΒψΘ°
Θ®1Θ©Β±÷±œΏ”κΓ―Oœύ«– ±Θ§«σ≥ωΒψMΒΡΉχ±ξΚΆΒψPΒΡΉχ±ξΘΜ
Θ®2Θ©»γΆΦ2Θ§Β±ΒψP‘ΎœΏΕΈOA…œ ±Θ§÷±œΏ1”κΓ―OΫΜ”ΎEΘ§FΝΫΒψΘ®ΒψE‘ΎΒψFΒΡ…œΖΫΘ©ΙΐΒψFΉςFCΓΈx÷αΘ§”κΓ―OΫΜ”ΎΝμ“ΜΒψCΘ§Ν§ΫαECΫΜy÷α”ΎΒψDΘ°
ΔΌ»γΆΦ3Θ§»τΒψP”κΒψA÷ΊΚœ ±Θ§«σODΒΡ≥Λ≤Δ–¥≥ωΫβ¥πΙΐ≥ΧΘΜ
ΔΎ»γΆΦ2Θ§»τΒψP”κΒψA≤Μ÷ΊΚœ ±Θ§ODΒΡ≥Λ «ΖώΖΔ…ζ±δΜ·Θ§»τ≤ΜΖΔ…ζ±δΜ·Θ§«κ«σ≥ωODΒΡ≥Λ≤Δ–¥≥ωΫβ¥πΙΐ≥ΧΘΜ»τΖΔ…ζ±δΜ·Θ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©»γΆΦ4Θ§‘ΎΘ®2Θ©ΒΡΜυ¥Γ…œΘ§Ν§ΫαBFΘ§ΫΪœΏΕΈBF»ΤΒψBΡφ ±’κ–ΐΉΣ90ΓψΒΫBQΘ§»τΒψQ‘ΎCEΒΡ―”≥ΛœΏ ±Θ§«κ”ΟΒ» Ϋ÷±Ϋ”±μ ΨœΏΕΈFCΘ§FQ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―ß–Θ÷≤Έο‘Α―Ί¬ΖΜΛάΗΒΡΈΤ Έ≤ΩΖ÷…ηΦΤ≥…»τΗ…Ηω»ΪΒ»Νβ–ΈΆΦΑΗΘ§ΟΩ‘ωΦ”“ΜΗωΝβ–ΈΆΦΑΗΘ§ΈΤ Έ≥ΛΕ»ΨΆ‘ωΦ”dcmΘ§»γΆΦΥυ ΨΘ§“―÷ΣΟΩΗωΝβ–ΈΆΦΑΗΒΡ±Ώ≥ΛΈΣ10![]() cmΘ§Τδ÷–“ΜΗωΡΎΫ«ΈΣ60ΓψΘ°
cmΘ§Τδ÷–“ΜΗωΡΎΫ«ΈΣ60ΓψΘ°
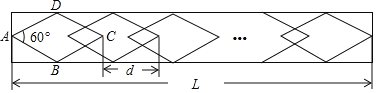
(1)«σ“ΜΗωΝβ–ΈΆΦΑΗΥ°ΤΫΖΫœρΒΡΕ‘Ϋ«œΏ≥ΛΘΜ
(2)»τdΘΫ26Θ§ΈΤ ΈΒΡ≥ΛΕ»LΡήΖώ «6010cmΘΩ»τΡήΘ§«σ≥ωΝβ–ΈΗω ΐΘΜ»τ≤ΜΡήΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫΪΝΫΩι÷±Ϋ«»ΐΫ«Αε»γΆΦ1Ζ≈÷ΟΘ§Β»―ϋ÷±Ϋ«»ΐΫ«Αε![]() ΒΡ÷±Ϋ«ΕΞΒψ «Βψ
ΒΡ÷±Ϋ«ΕΞΒψ «Βψ![]() Θ§
Θ§![]() Θ§÷±Ϋ«Αε
Θ§÷±Ϋ«Αε![]() ΒΡ÷±Ϋ«ΕΞΒψ
ΒΡ÷±Ϋ«ΕΞΒψ![]() ‘Ύ
‘Ύ![]() …œΘ§«“
…œΘ§«“![]() Θ§
Θ§![]() Θ°»ΐΫ«Αε
Θ°»ΐΫ«Αε![]() ΙΧΕ®≤ΜΕ·Θ§ΫΪ»ΐΫ«Αε
ΙΧΕ®≤ΜΕ·Θ§ΫΪ»ΐΫ«Αε![]() »ΤΒψ
»ΤΒψ![]() Ρφ ±’κ–ΐΉΣΘ§–ΐΉΣΫ«ΈΣ
Ρφ ±’κ–ΐΉΣΘ§–ΐΉΣΫ«ΈΣ![]()
![]() Θ°
Θ°
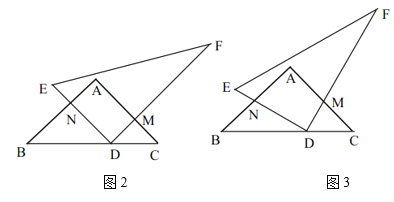
Θ®1Θ©Β±![]() _______ ±Θ§
_______ ±Θ§![]() ΘΜ
ΘΜ
Θ®2Θ©Β±![]() ±Θ§»ΐΫ«Αε
±Θ§»ΐΫ«Αε![]() »ΤΒψ
»ΤΒψ![]() Ρφ ±’κ–ΐΉΣ÷Ν»γΆΦ2ΈΜ÷ΟΘ§…η
Ρφ ±’κ–ΐΉΣ÷Ν»γΆΦ2ΈΜ÷ΟΘ§…η![]() ”κ
”κ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§
Θ§![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§«σΥΡ±Ώ–Έ
Θ§«σΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΘ°
ΒΡΟφΜΐΘ°
Θ®3Θ©»γΆΦ3Θ§…η![]() Θ§ΥΡ±Ώ–Έ
Θ§ΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§«σ
Θ§«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡ±μ¥ο ΫΘ®≤Μ”Ο–¥
ΒΡ±μ¥ο ΫΘ®≤Μ”Ο–¥![]() ΒΡ»Γ÷ΒΖΕΈßΘ©Θ°
ΒΡ»Γ÷ΒΖΕΈßΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
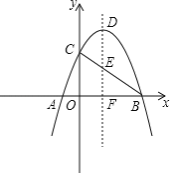
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏ![]() ”κx÷αœύΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎCΘ§ΕΞΒψΈΣDΘ§≈ΉΈοœΏΒΡΕ‘≥Τ÷αDF”κBCœύΫΜ”ΎΒψEΘ§”κx÷αœύΫΜ”ΎΒψFΘ°
”κx÷αœύΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎCΘ§ΕΞΒψΈΣDΘ§≈ΉΈοœΏΒΡΕ‘≥Τ÷αDF”κBCœύΫΜ”ΎΒψEΘ§”κx÷αœύΫΜ”ΎΒψFΘ°
Θ®1Θ©«σœΏΕΈDEΒΡ≥ΛΘΜ
Θ®2Θ©…ηΙΐEΒΡ÷±œΏ”κ≈ΉΈοœΏœύΫΜ”ΎM(x1Θ§y1)Θ§N(x2Θ§y2)Θ§ ‘≈–ΕœΒ±|x1©¹x2|ΒΡ÷ΒΉν–Γ ±Θ§÷±œΏMN”κx÷αΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©…ηPΈΣx÷α…œΒΡ“ΜΒψΘ§ΓœDAO+ΓœDPO=ΓœΠΝΘ§Β±tanΓœΠΝ=4 ±Θ§«σΒψPΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com