
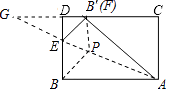
【题目】矩形纸片ABCD中,AB=5,AC=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为 . 
【答案】![]()
【解析】解:如图所示,设PF⊥CD,
∵BP=FP,
由翻折变换的性质可得BP=B′P,
∴FP=B′P,
∴FP⊥CD,
∴B′,F,P三点构不成三角形,
∴F,B′重合分别延长AE,CD相交于点G,
∵AB∥CD,
∴∠BAG=∠AGD,
∵∠BAG=∠B′AG,
∴∠AGD=∠B′AG,
∴GB′=AB′=AB=5,
∵PB′(PF)⊥CD,
∴PB′∥AC,
∴△ACG∽△PB′G,
∵Rt△ACB′中,AB′=AB=5,AC=3,
∴B′C= ![]() =4,
=4,
∴CB′=5﹣4=1,CG=CB′+B′G=4+5=9,
∴△ACG与△PB′G的相似比为9:5,
∴AC:PB′=9:5,
∵AC=3,
∴PB′= ![]() .
.
所以答案是: ![]() .
.
【考点精析】通过灵活运用翻折变换(折叠问题),掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于50棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M点N的距离相等,则x= .
(2)数轴上是否存在点P,使点P到点M、点N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
(3)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕![]() )的值;
)的值;
(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形ABCD是“阳光小区”内一块空地,已知AB=(2a+6b)米,BC=(8a+4b)米.
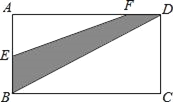
(1)该长方形ABCD的面积是多少平方米?
(2)若E为AB边的中点,DF=![]() BC,现打算在阴影部分种植一片草坪,这片草坪的面积是多少平方米?
BC,现打算在阴影部分种植一片草坪,这片草坪的面积是多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 . 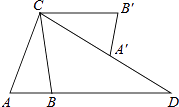
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com