
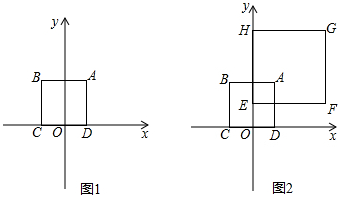
���� ��1�����ݡ��Ⱦ�Բ���Ķ��壬��ֻ֪ҪԲ���������ε����ģ����������εġ��Ⱦ�Բ����Ҳ����˵Բ�������������ĵľ������Բ�İ뾶���ɣ��Ӷ������ж��ĸ�����Գ�Ϊ������ABCD�ġ��Ⱦ�Բ����Բ�ģ�������Խ����
��2�����������֪��ֻҪ�����P��������ABCD�����ĵľ��뼴����ð뾶r�ij��ȣ�����PE�����Եõ�ֱ��PE�Ľ���ʽ������B�Ƿ��ڴ�ֱ���ϣ���BE��ֱ��AC�Ĺ��Ŀ����ж�PE��ֱ��AC�Ĺ�ϵ��������Խ����
��3���������⣬���Եõ���P������������г���Ӧ�Ķ�Ԫһ�η����飬�Ӷ�������õ�P�����꣮
��� �⣺��1������AC��BD�ཻ�ڵ�M������ͼ1��ʾ��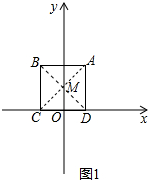
���ı���ABCD�������Σ�
���M��������ABCD�����ģ����ıߵľ�����ȣ�
���Pһ������M��
��������ABCD�Ķ���A������Ϊ��2��4��������C��D��x���ϣ��ҵ�C�ڵ�D����࣮
���M��0��2����
���P��Բ�������ǣ�x��y����
�ࣨx-0��2+��y-2��2=��2 $\sqrt{2}$��2��
��P1��0��2����P2��-2��4����P3��4 $\sqrt{2}$��2����P4��0��2-2$\sqrt{2}$���ֱ��������ķ��̣�ֻ��P2��-2��4����P4��0��2-2$\sqrt{2}$��������
�ʴ�Ϊ��P2��-2��4����P4��0��2-2$\sqrt{2}$����
��2��������ɵã�
��M��������0��2������P��-3��6����
��r=$\sqrt{��-3-0��^{2}+��6-2��^{2}}$=5��
����P������Ϊ��-3��6������P�İ뾶r��5ʱ����P��������ABCD�ġ��Ⱦ�Բ����
�ʴ�Ϊ5��
��ʱ��P��ֱ��AC��λ�ù�ϵ���ཻ��
���ɣ���������ABCD�Ķ���A������Ϊ��2��4��������C��D��x���ϣ��ҵ�C�ڵ�D����࣬
���C��-2��0����
�����A��2��4������C��-2��0����ֱ�ߵĽ���ʽΪy=kx+b��
�� $\left\{\begin{array}{l}{2k+b=4}\\{-2k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪ��y=x+2��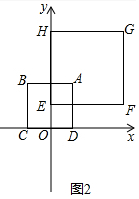
���P��-3��6����ֱ��AC�ľ���Ϊ��$\frac{|-3-6+2|}{\sqrt{{1}^{2}+��-1��^{2}}}$=$\frac{7\sqrt{2}}{2}$��
��$\frac{7\sqrt{2}}{2}$��5��
���ʱ��P��ֱ��AC��λ�ù�ϵ���ཻ��
��3�����P������Ϊ��x��y��������HF��EG���ڵ�N�����NΪ������EFGH�����ģ���ͼ2��ʾ��
�ߵ�E��0��2����N��3��5������C��-2��0������B��-2��4������PͬʱΪ�������������εġ��Ⱦ�Բ��������BC����ֱ�����У�
��$\left\{\begin{array}{l}{\sqrt{��x-0��^{2}+��2-y��^{2}}=\sqrt{��3-x��^{2}+��5-y��^{2}}}\\{\sqrt{��x-0��^{2}+��2-y��^{2}}=x-��-2��}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=5+2\sqrt{5}}\\{y=-2\sqrt{5}}\end{array}\right.$��$\left\{\begin{array}{l}{x=5-2\sqrt{5}}\\{y=2\sqrt{5}}\end{array}\right.$��
����P��Բ��P�������ǣ�5+2 $\sqrt{5}$��-2$\sqrt{5}$����5-2$\sqrt{5}$��2$\sqrt{5}$����
���� ���⿼��Բ���ۺ��⣬����Ĺؼ�����ȷ���⣬������Ŀ�������������������ʵĸ����ߣ��ҳ�����������Ҫ���������������ν�ϵ�˼�������⣮


 ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���֪��ABC=90�㣬��ACB=60�㣬DE��б��AC���д��ߣ��ֱ�AB��AC�ڵ�D��E������DC����BD=2�����߶�AC�ij���
��ͼ����Rt��ABC�У���֪��ABC=90�㣬��ACB=60�㣬DE��б��AC���д��ߣ��ֱ�AB��AC�ڵ�D��E������DC����BD=2�����߶�AC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
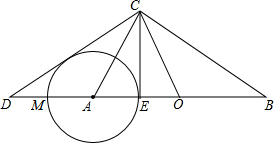 ��ͼ���ڡ�ABC���OCD�У���ACB=��DCO=90�㣬OΪAB���е㣮
��ͼ���ڡ�ABC���OCD�У���ACB=��DCO=90�㣬OΪAB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
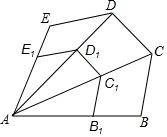 ��ͼ��BC��B1C1��CD��C1D1��DE��D1E1����BCD=118�㣬��CDE=119�㣬���B1C1D1����C1D1E1�Ķ�����
��ͼ��BC��B1C1��CD��C1D1��DE��D1E1����BCD=118�㣬��CDE=119�㣬���B1C1D1����C1D1E1�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com