
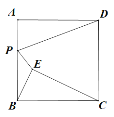
【题目】如图,已知正方形ABCD的边长为8,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是AB边上一动点,连接 PD,PE,则PD+PE长度的最小值为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
根据正方形的性质得到∠ABC=90°,推出∠BEC=90°,得到点E在以BC为直径的半圆上移动,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形AFGB,则点D的对应点是F,连接FO交AB于P,交⊙O于E,则线段EF的长即为PD+PE的长度最小值,根据勾股定理即可得到结论.
解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵∠ABE=∠BCE,
∴∠BCE+∠CBE=90°,
∴∠BEC=90°,
∴点E在以BC为直径的半圆上移动,
如图,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形AFGB,则点D的对应点是F,
连接FO交AB于P,交半圆O于E,则线段EF的长即为PD+PE的长度最小值,OE=4,
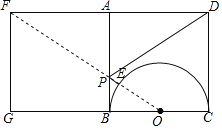
∵∠G=90°,FG=BG=AB=8,
∴OG=12,
![]() (勾股定理),
(勾股定理),
∴![]() ,
,
∴PD+PE的长度最小值为![]() ,
,
故选D.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】服装专卖店计划购进A,B两种型号的精品女装.已知3件A型女装和2件B型女装共需5400元;2件A型女装和1件B型女装共需3200元.
(1)求A,B两种型号女装的单价;
(2)专卖店购进A,B两种型号的女装共60件,其中A型的件数不少于B型件数的2倍,如果B型打八折,那么该专卖店至少需要准备多少货款.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
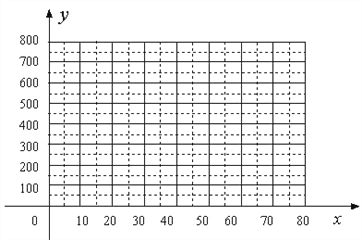
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
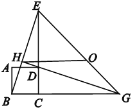
【题目】如图,四边形ABCD是正方形,ΔECG是等腰直角三角形,∠BGE的平分线过点D交BE 于H,O是EG的中点,对于下面四个结论:①GH⊥BE;②OH∥BG,且![]() ;③
;③![]() ;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次商业足球比赛中,门票销售单位对团体购买门票实行优惠,决定在原定票价基础上每张降价100元,这样按原定票价需花费14 000元购买的门票张数,现在只花费了10 500元.
(1)求每张门票的原定票价;
(2)根据实际情况,组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元?
(3)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入不透明的盒子中摇匀.
(1)从中随机抽出1张卡片,抽出的卡片上的数字恰好是偶数的概率为 .
(2)从中随机抽出1张卡片,记录数字后放回摇匀,再抽出一张卡片,记录数字.用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解初中学生参加综合实践活动的情况,随机抽取了本市初一、初二、初三年级各![]() 名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.
名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.
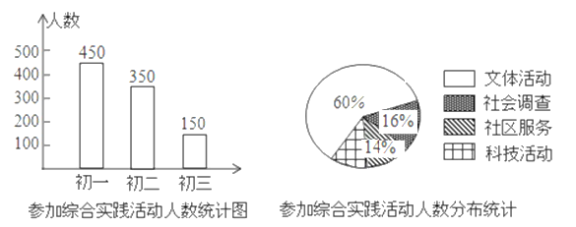
(1)在被调查的学生中,参加综合实践活动的有多少人,参加科技活动的有多少人;
(2)如果本市有![]() 万名初中学生,请你估计参加科技活动的学生约有多少名.
万名初中学生,请你估计参加科技活动的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,锐角△ABC中,D、E分别是AB、BC的中点,F是AC上的点,且∠AFE=∠A,DM//EF交AC于点M.
(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图2,
① 求证:△DEG∽△ECF;
② 从线段CE上取一点H,连接FH使∠CFH=∠B,若BG=1,求EH的长.
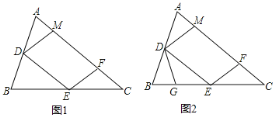
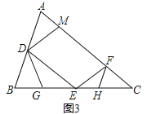
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com