
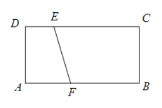
【题目】如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是________.
【答案】0或1<AF<![]() 或4.
或4.
【解析】
先根据圆周角定理确定点P在以EF为直径的圆O上,且是与矩形ABCD的交点,当F与A和B重合时,有两个直角三角形,都符合条件,即AF=0或4,再找⊙O与AD和BC相切时AF的长,此时⊙O与矩形边各有一个交点或三个交点,在之间运动过程中符合条件,确定AF的取值.
解:以EF为斜边的直角三角形的直角顶点P是以EF为直径的圆与矩形边的交点, 取EF的中点O,
(1) 如图1, 当圆O与AD相切于点G时, 连结OG, 此时点G与点P重合,只有一个点, 此时AF=OG=DE=1;

(2) 如图2,

当圆O与BC相切于点G, 连结OG,EG, FG, 此时有三个点P可以构成Rt△EFP,
∵OG是圆O的切线,∴OG⊥BC
∴OG∥AB∥CD
∵OE=OF,
∴BG=CG,∴OG=![]() (BF+CE),
(BF+CE),
设AF=x, 则BF=4-x, OG=![]() (4-x+4-1)=
(4-x+4-1)= ![]() (7-x)
(7-x)
则EF=2OG=7-x, EG![]() =EC
=EC![]() +CG
+CG![]() =9+1=10,FG
=9+1=10,FG![]() =BG
=BG![]() +BF
+BF![]() =1+(4-x)
=1+(4-x) ![]() ,
,
在Rt△EFG中, 由勾股定理得EF![]() =EG
=EG![]() +FG
+FG![]() ,
,
得(7-x) ![]() =10+1+(4-x)2,解得x=
=10+1+(4-x)2,解得x=![]() ,
,
所以当1<AF<![]() 时,以EF为直径的圆与矩形ABCD的交点 (除了点E和F) 只有两个;
时,以EF为直径的圆与矩形ABCD的交点 (除了点E和F) 只有两个;
(3)因为点F是边AB上一动点:
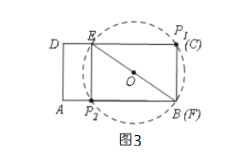
当点F与B点重合时, AF=4, 此时Rt△EFP正好有两个符合题意,如图3;
故答案为0或1<AF< ![]() 或4.
或4.


科目:初中数学 来源: 题型:
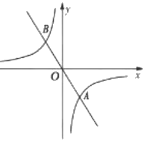
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= -2x和反比例函数![]() 的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线
的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线![]() 交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量山坡上一棵树PQ的高度,小明在点A处利用测角仪测得树顶P的仰角为450 ,然后他沿着正对树PQ的方向前进10m到达B点处,此时测得树顶P和树底Q的仰角分别是600和300,设PQ垂直于AB,且垂足为C.
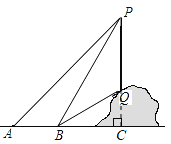
(1)求∠BPQ的度数;
(2)求树PQ的高度(结果精确到0.1m, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.
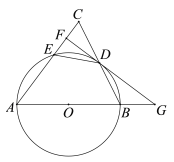
(1)求证:GD为⊙O切线;
(2)求证:DE2=EF·AC;
(3)若tan∠C=2,AB=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟于中秋节前![]() 天里销售某品牌月饼,其进价为
天里销售某品牌月饼,其进价为![]() 元/
元/![]() .设第
.设第![]() 天的销售价格为
天的销售价格为![]() (元/
(元/![]() ),销售量为
),销售量为![]() .该超市根据以往的销售经验得出以下的销售规律:①当
.该超市根据以往的销售经验得出以下的销售规律:①当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 与
与![]() 满足一次函数关系,且当
满足一次函数关系,且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .②
.②![]() 与
与![]() 的关系为
的关系为![]() .
.
(1)当![]() 时,
时,![]() 与
与![]() 的关系式为 ;
的关系式为 ;
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)若超市希望第![]() 天到第
天到第![]() 天的日销售利润
天的日销售利润![]() (元)随
(元)随![]() 的增大而增大,则需要在当天销售价格的基础上涨
的增大而增大,则需要在当天销售价格的基础上涨![]() 元/
元/![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形AOBC中,对角线交于点E,双曲线y=![]() (k>0)经过A、E两点,若平行四边形AOBC的面积为24,则k的值是( )
(k>0)经过A、E两点,若平行四边形AOBC的面积为24,则k的值是( )
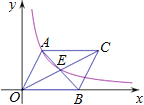
A. 8B. 7.5C. 6D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
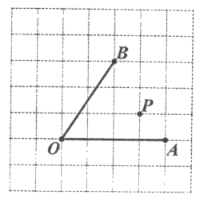
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上.I.
均在格点上.I. ![]() 的长等于______________;Ⅱ.点
的长等于______________;Ⅱ.点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上,当
上,当![]() 的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出
的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出![]() ,并简要说明点
,并简要说明点![]() ,
,![]() 的位置是如何找到的(不要求证明)____________ .
的位置是如何找到的(不要求证明)____________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com