
【题目】如图,已知在![]() 中,点
中,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长,交
并延长,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() .
.
(2)连接![]() ,
,![]() ,当
,当![]() ______时,四边形
______时,四边形![]() 是正方形.请说明理由.
是正方形.请说明理由.
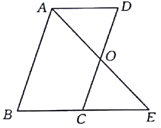
【答案】(1)见解析(2)45°
【解析】
(1)根据平行线的性质可得∠D=∠OCE,∠DAO=∠E,再根据中点定义可得DO=CO,然后可利用AAS证明△AOD≌△EOC;
(2)当∠B=∠AEB=45°时,四边形ACED是正方形,首先证明四边形ACED是平行四边形,再证对角线互相垂直且相等可得四边形ACED是正方形.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
∵O是CD的中点,
∴OC=OD,
在△ADO和△ECO中,
 ,
,
∴△AOD≌△EOC(AAS);
(2)当∠B=∠AEB=45°时,四边形ACED是正方形.如图;

∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,
∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.
∴ACED是菱形.
∵AB=AE,AB=CD,
∴AE=CD.
∴菱形ACED是正方形.
故答案为:45.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′,其中点B的运动路径为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
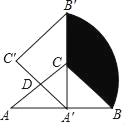
A.![]() π﹣
π﹣![]() B.2C.
B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
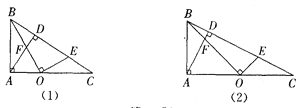
【题目】如图(1),在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上的一点,连接BO交AD于点F,OE⊥OB交BC边于点E.
(1)试说明:△ABF∽△COE.
(2)如图(2),当O为AC边的中点,且![]() 时,求
时,求![]() 的值.
的值.
(3)当O为AC边的中点,![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,E为AC上一点,连接BE,将△BEC旋转,使点C落在BC上的点D处,点B落在BC上方的点F处,点E落在点C处,连接AF.求证:四边形ABDF为平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在利用图象法求方程x2=![]() x+3的解x1,x2时,下面是四位同学的解法:
x+3的解x1,x2时,下面是四位同学的解法:
甲:函数y=x2﹣![]() x﹣3的图象与x轴交点的横坐标是x1,x2
x﹣3的图象与x轴交点的横坐标是x1,x2
乙:函数y=x2与y=![]() x+3的图象交点的横坐标是x1,x2
x+3的图象交点的横坐标是x1,x2
丙:函数y=x2﹣3与y=![]() x的图象交点的横坐标是x1,x2
x的图象交点的横坐标是x1,x2
丁:函数y=x2+1与y=![]() x+4的图象交点的横坐标是x1,x2
x+4的图象交点的横坐标是x1,x2
你认为解法正确的同学有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 三个顶点的坐标分别为A(2,3)、B(1,1)、C(5,1).
三个顶点的坐标分别为A(2,3)、B(1,1)、C(5,1).
(1)把![]() 平移后,其中点
平移后,其中点![]() 移到点
移到点![]() ,面出平移后得到的
,面出平移后得到的![]() ;
;
(2)把![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,画出旋转后得到的
,画出旋转后得到的![]() ,并求出旋转过程中点
,并求出旋转过程中点![]() 经过的路径长(结果保留根号和
经过的路径长(结果保留根号和![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分7分)
四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树状图法说明理由,若认为不公平,请你修改规则,使游戏变得公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
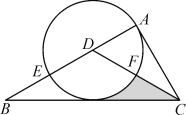
【题目】如图,在Rt△ABC中,∠BAC=90°,CD平分∠ACB,交AB于点D,以点D为圆心,DA为半径的圆与AB相交于点E,与CD交于点F.
(1)求证:BC是⊙D的切线;
(2)若EF∥BC,且BC=6,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com