
【题目】(11分)已知△ABC,分别以AB、BC、CA为边向形外作等边三角形ABD、等边三角形BCE、等边三角形ACF.
(1)如图1,当△ABC是等边三角形时,请你写出满足图中条件,四个成立的结论;
(2)如图2,当△ABC中只有∠ACB=60°时,请你证明S△ABC与S△ABD的和等于S△BCE与S△ACF的和.


【答案】(1)答案不唯一,如:DE=EF,DF=EF,∠D=∠E=∠F,A、B、C分别为DF、DE、EF的中点;(2)见解析
【解析】试题分析:(1)由等边三角形的性质可写出结论.
(2)要证明以上结论,需创造一些条件,首先可从△ABC中分出一部分使得与△ACF的面积相等,则过A作AM∥FC交BC于M,连接DM、EM,就可创造出这样的条件,然后再证其它的面积也相等即可.
试题解析:(1)DE=EF,DF=EF,∠D=∠E=∠F,A、B、C分别为DF、DE、EF的中点;
(2)过A作AM∥FC交BC于M,连接DM、EM,
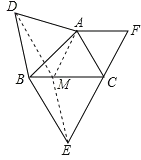
∵∠ACB=60°,∠CAF=60°,
∴∠ACB=∠CAF,
∴AF∥MC,
∴四边形AMCF是平行四边形,
又∵FA=FC,
∴四边形AMCF是菱形,
∴AC=CM=AM,且∠MAC=60,
∵在△BAC与△EMC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△BAC≌△EMC,
∵∠DAM=∠DAB+∠BAM=60°+∠BAM,
∠BAC=∠MAC+∠BAM=60°+∠BAM,
∴∠BAC=∠DAM
在△ABC和△ADM中
AB=AD,∠BAC=∠DAM,AC=AM,
∴△ABC≌△ADM(SAS)
故△ABC≌△MEC≌△ADM,
在CB上截取CM,使CM=CA,
再连接AM、DM、EM
易证△AMC为等边三角形,
在△ABC与△MEC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△ABC≌△MEC(SAS),
∴AB=ME,∠ABC=∠MEC,
又∵DB=AB,
∴DB=ME,
∵∠DBC=∠DBA+∠ABC=60°+∠ABC,
∠BME=∠BCE+∠MEC=60°+∠MEC,
∴∠DBC=∠BME,
∴DB∥ME,
即DB与ME平行且相等,故四边形DBEM是平行四边形,
∴四边形DBEM是平行四边形,
∴S△BDM+S△DAM+S△MAC=S△BEM+S△EMC+S△ACF,
即S△ABC+S△ABD=S△BCE+S△ACF.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为 ![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分,摸到蓝球得2分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到一个问题:5个同样大小的正方形纸片排列形式如图1所示,将它们分割后拼接成一个新的正方形.他的做法是:按图2所示的方法分割后,将三角形纸片①绕AB的中点O旋转至三角形纸片②处,以此方法继续操作,即可拼成一个新的正方形DEFG.




请你参考小明的做法解决下列问题:
(1)现有5个形状,大小相同的矩形纸片,排列形式如图3所示.请将其分割后拼接成一个平行四边形,要求:在图3中画出并指明拼接成的平行四边形(画出一个符合条件的平行四边形即可).
(2)如图4,在面积为2的平行四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,分别连结AF、BG、CH、DE,所得□MNPQ面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式的规律,解答下列问题:
a1=![]() ,a2=
,a2=![]() (
(![]() ),a3=
),a3=![]() (
(![]() ),a4=
),a4=![]() (
(![]() ),…….
),…….
(1)第5个等式为 ;第n个等式为 (用含n的代数式表示,n为正整数);
(2)设S1=a1﹣a2,S2=a3﹣a4,S3=a5﹣a6,……,S1008=a2015﹣a2016.求S1+S2+S3+……+S1008的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )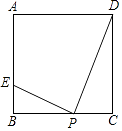
A.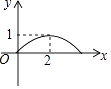
B.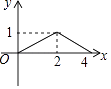
C.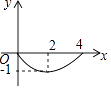
D.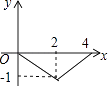
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
(1)∠DFM=∠BEN;
(2)四边形MENF是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com