
如图,点 是
是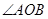 的边
的边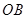 上的一点.
上的一点.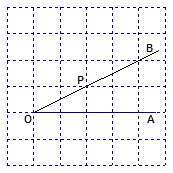
①过点 画OB的垂线,交
画OB的垂线,交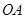 于点C;
于点C;
②过点P画OA的垂线,垂足为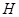 ;
;
③线段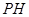 的长度是点
的长度是点 到直线 的距离, 是点
到直线 的距离, 是点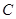 到直线
到直线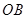 的距离;因为 ,所以线段
的距离;因为 ,所以线段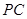 、
、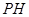 、
、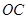 这三条线段大小关系是 (用“<”号连接)
这三条线段大小关系是 (用“<”号连接)
①如图所示 ②如图所示(标注要正确) 
③直线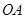 ,线段
,线段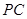 ,垂线段最短,
,垂线段最短,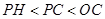
解析试题分析:过一点有且只有一条垂线,做垂线时可以用三角板的直角边辅助作画。过点P作OB的垂线,交OA于点C,即是作CP⊥OB,同理,过点P作OA的垂线,垂足于H,即作PH⊥OA.点到直线的长度即是距离,也就是垂线段,所以PH的长度是点P到直线OA的距离,线段PC是点C到直线OB的距离。根据垂线段最短,可以比较PC、PH、OC这三条线段的大小关系,PH<PC<OP,OP<OC,所以PH<PC<OC.
考点:垂线段的定义和性质
点评:垂线和垂线段的区别,前者是直线,后者是线段、有长度。过一点到直线的所有连线中,垂线段最短。


科目:初中数学 来源: 题型:
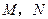 分别在正△
分别在正△ 的
的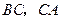 边上,且
边上,且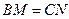 ,
, 交于点
交于点 .
.
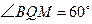 .
.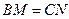 ”与“
”与“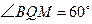 ”的位置交换,得到的是否仍是真命题?
”的位置交换,得到的是否仍是真命题?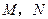 分别移动到
分别移动到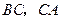 的延长线上,是否仍能得到
的延长线上,是否仍能得到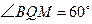 ?
?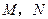 分别在正三角形
分别在正三角形 的
的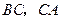 边上”改为“点
边上”改为“点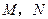 分别在正方形
分别在正方形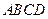 的
的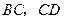 边上”,是否仍能得到
边上”,是否仍能得到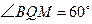 ?……
?……查看答案和解析>>
科目:初中数学 来源:2010-2011学年辽宁省大连第76中学八年级数学10月单元测试试卷 题型:解答题
学完“等腰三角形”一章后,老师布置了一道思考题:如图,点 分别在正△
分别在正△ 的
的 边上,且
边上,且 ,
, 交于点
交于点 .
.
【小题1】求证: .
.
【小题2】做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“ ”与“
”与“ ”的位置交换,得到的是否仍是真命题?
”的位置交换,得到的是否仍是真命题?
②若将题中的点 分别移动到
分别移动到 的延长线上,是否仍能得到
的延长线上,是否仍能得到 ?
?
③若将题中的条件“点 分别在正三角形
分别在正三角形 的
的 边上”改为“点
边上”改为“点 分别在正方形
分别在正方形 的
的 边上”,是否仍能得到
边上”,是否仍能得到 ?……
?……
请你作出判断,是的填“是”,否的算出度数填在横线上,① ;② ;③ .画图并证明 ②.
查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(江苏连云港卷)数学(带解析) 题型:解答题
如图1,点 将线段
将线段 分成两部分,如果
分成两部分,如果 ,那么称点
,那么称点 为线段
为线段 的黄金分割点.
的黄金分割点.
某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线 将一个面积为
将一个面积为 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为 ,
, ,如果
,如果 ,那么称直线
,那么称直线 为该图形的黄金分割线.
为该图形的黄金分割线.
(1)研究小组猜想:在 中,若点
中,若点 为
为 边上的黄金分割点(如图2),则直线
边上的黄金分割点(如图2),则直线 是
是 的黄金分割线.你认为对吗?为什么?
的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点 任作一条直线交
任作一条直线交 于点
于点 ,再过点
,再过点 作直线
作直线 ,交
,交 于点
于点 ,连接
,连接 (如图3),则直线
(如图3),则直线 也是
也是 的黄金分割线.
的黄金分割线.
请你说明理由.
(4)如图4,点 是
是 的边
的边 的黄金分割点,过点
的黄金分割点,过点 作
作 ,交
,交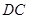 于点
于点 ,显然直线
,显然直线 是
是 的黄金分割线.请你画一条
的黄金分割线.请你画一条 的黄金分割线,使它不经过
的黄金分割线,使它不经过 各边黄金分割点.
各边黄金分割点.
查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(江苏连云港卷)数学(解析版) 题型:解答题
如图1,点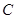 将线段
将线段 分成两部分,如果
分成两部分,如果 ,那么称点
,那么称点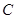 为线段
为线段 的黄金分割点.
的黄金分割点.
某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线 将一个面积为
将一个面积为 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为 ,
, ,如果
,如果 ,那么称直线
,那么称直线 为该图形的黄金分割线.
为该图形的黄金分割线.

(1)研究小组猜想:在 中,若点
中,若点 为
为 边上的黄金分割点(如图2),则直线
边上的黄金分割点(如图2),则直线 是
是 的黄金分割线.你认为对吗?为什么?
的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点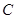 任作一条直线交
任作一条直线交 于点
于点 ,再过点
,再过点 作直线
作直线 ,交
,交 于点
于点 ,连接
,连接 (如图3),则直线
(如图3),则直线 也是
也是 的黄金分割线.
的黄金分割线.
请你说明理由.
(4)如图4,点 是
是 的边
的边 的黄金分割点,过点
的黄金分割点,过点 作
作 ,交
,交 于点
于点 ,显然直线
,显然直线 是
是 的黄金分割线.请你画一条
的黄金分割线.请你画一条 的黄金分割线,使它不经过
的黄金分割线,使它不经过 各边黄金分割点.
各边黄金分割点.
查看答案和解析>>
科目:初中数学 来源:2012届辽宁省八年级数学10月单元测试试卷 题型:解答题
学完“等腰三角形”一章后,老师布置了一道思考题:如图,点 分别在正△
分别在正△ 的
的 边上,且
边上,且 ,
, 交于点
交于点 .
.

1.求证: .
.
2.做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“ ”与“
”与“ ”的位置交换,得到的是否仍是真命题?
”的位置交换,得到的是否仍是真命题?
②若将题中的点 分别移动到
分别移动到 的延长线上,是否仍能得到
的延长线上,是否仍能得到 ?
?
③若将题中的条件“点 分别在正三角形
分别在正三角形 的
的 边上”改为“点
边上”改为“点 分别在正方形
分别在正方形 的
的 边上”,是否仍能得到
边上”,是否仍能得到 ?……
?……
请你作出判断,是的填“是”,否的算出度数填在横线上,① ;② ;③ .画图并证明 ②.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com