考点:抛物线与x轴的交点
专题:计算题
分析:分类讨论:当a-1=0,即a=1,函数解析式为y=-2x+1,函数图象为直线,与x轴只有一个交点;当a-1≠0,函数图象为抛物线,△=(-2)2-4(a-1)=0,
解得a=2.
解答:解:当a-1=0,即a=1,函数解析式为y=-2x+1,此直线与x轴的交点坐标为(
,0),
当a-1≠0,△=(-2)
2-4(a-1)=0,解得a=2,即a=2时,抛物线与x轴只有一个交点.
所以a的值为1或2.
故答案为1或2.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.



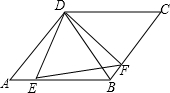 如图所示,在平行四边形ABCD中,∠A=60°,CD=BC,E,F分别在AB和BC上,且∠EDF=60°.
如图所示,在平行四边形ABCD中,∠A=60°,CD=BC,E,F分别在AB和BC上,且∠EDF=60°.