
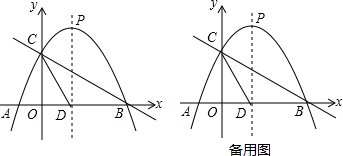
分析 (1)由待定系数法建立二元一次方程组求出m、n的值即可;
(2)由(1)的解析式求出顶点坐标,再由勾股定理求出CD的值,设出点E坐标,表示出DE,CE,由等腰三角形的性质及勾股定理就可以求出结论;
(3)①先求出BC的解析式,设出E点的坐标为(m,-$\frac{1}{2}$m+2),分三种情况讨论计算出m;
②设出点E的横坐标,由四边形CDBF的面积=S△BCD+S△CEF+S△BEF求出S与a的关系式,由二次函数的性质就可以求出结论.
解答 解(1)∵A(-1,0),B(4,0)在抛物线y=-$\frac{1}{2}$x2+mx+n,
∴$\left\{\begin{array}{l}{-\frac{1}{2}-m+n=0}\\{-\frac{1}{2}×16+4m+n=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=\frac{3}{2}}\\{n=2}\end{array}\right.$,
∴抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
(2)以PC为半径的圆与直线CD的位置关系是相切,
理由:由(1)得,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
∵与y轴交于点C,抛物线的对称轴交x轴于点D,
∴C(0,2),D($\frac{3}{2}$,0),
∵抛物线顶点为P点,
∴P($\frac{3}{2}$,$\frac{25}{8}$),
∴CD=$\frac{5}{2}$,PD=$\frac{25}{8}$,PC=$\frac{15}{8}$,
∴CD2+PC2=($\frac{5}{2}$)2+($\frac{15}{8}$)2=$\frac{625}{64}$=($\frac{25}{8}$)2=PD2,
∴PC⊥CD,
∵点C在圆上,
∴直线CD与PC为半径的圆相切;
(3)①∵B(4,0),C(0,2),
∴直线BC解析式为y=-$\frac{1}{2}$x+2,
设点E(m,-$\frac{1}{2}$m+2),(0<m≤4)
∵C(0,2),D($\frac{3}{2}$,0),
∴CE2=m2+$\frac{1}{4}$m2,DE2=(m-$\frac{3}{2}$)2+(-$\frac{1}{2}$m+2)2,CD2=$\frac{25}{4}$,
∵△ECD是等腰三角形
∴Ⅰ、当CE=DE时,即:CE2=DE2,
∴m2+$\frac{1}{4}$m2=(m-$\frac{3}{2}$)2+(-$\frac{1}{2}$m+2)2,
∴m=$\frac{5}{4}$,
∴E($\frac{5}{4}$,$\frac{11}{8}$),
Ⅱ、当CE=CD时,即:CE2=CD2,
∴m2+$\frac{1}{4}$m2=$\frac{25}{4}$,
∴m=$\sqrt{5}$或m=-$\sqrt{5}$(舍),
∴E($\sqrt{5}$,$\frac{4-\sqrt{5}}{2}$)
Ⅲ、当DE=CD时,即:CD2=DE2
∴(m-$\frac{3}{2}$)2+(-$\frac{1}{2}$m+2)2=$\frac{25}{4}$,
∴m=4或m=0(舍),
∴E(4,0),
②设出点E的横坐标为a,
∴EF=-$\frac{1}{2}$a2+2a(0≤a≤4),
∴S四边形CDBF=S△BCD+S△CEF+S△BEF
=$\frac{1}{2}$BD×OC+$\frac{1}{2}$EF×CM+$\frac{1}{2}$EF×BN
=$\frac{1}{2}$×$\frac{5}{2}$×2+$\frac{1}{2}$a(-$\frac{1}{2}$a2+2a)+$\frac{1}{2}$(4-a)(-$\frac{1}{2}$a2+2a)
=-a2+4a+$\frac{5}{2}$
=-(a-2)2+$\frac{13}{2}$,
∴当a=2时,S四边形CDBF的最大值为$\frac{13}{2}$,此时E(2,1).
点评 此题是二次函数综合题,主要考查了待定系数法求一次函数的解析式的运用,二次函数的解析式的运用,勾股定理的运用,等腰三角形的性质的运用,四边形的面积的运用,解答时求出函数的解析式是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.573×10-5 | B. | 5.73×10-5 | C. | 5.73×10-6 | D. | 0.573×10-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
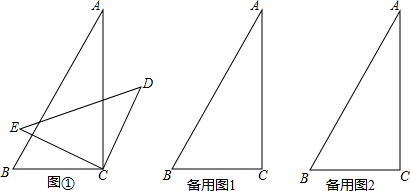
 如图(1),AB∥CD,猜想∠BPD与∠B、∠D的数量关系,并说明理由.
如图(1),AB∥CD,猜想∠BPD与∠B、∠D的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这个球一定是黑球 | |
| B. | 摸到黑球、白球的可能性的大小一样 | |
| C. | 这个球可能是白球 | |
| D. | 事先能确定摸到什么颜色的球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
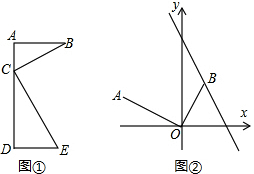 探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):
探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com