
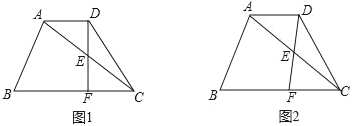
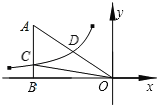
【题目】已知在梯形ABCD中,AD∥BC,AC=BC=10,cos∠ACB=![]() ,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
(1)如图1,当DF⊥BC时,求AD的长;
(2)设EC=y,求y关于x的函数解析式,并直接写出定义域;
(3)当△DFC是等腰三角形时,求AD的长.
【答案】(1)AD=![]() ;(2)y=
;(2)y=![]() x2﹣
x2﹣![]() x+10(0<x≤10);(3)AD的长为6和
x+10(0<x≤10);(3)AD的长为6和![]() .
.
【解析】
(1)证明△ADC∽△DCE,利用ACCE=CD2=DF2+FC2=36+16a2=105a,即可求解;
(2)过点C作CH⊥AD交AD的延长线于点H,CD2=CH2+DH2=(ACsinα)2+(ACcosα﹣x)2,即可求解;
(3)分DF=DC、FC=DC、FC=FD三种情况,求解即可.
(1)设∠ACB=∠EDC=∠α=∠CAD,
∵cosα=![]() ,
,
∴sinα=![]() ,
,
过点A作AH⊥BC交于点H,
AH=ACsinα=6=DF,BH=2,

如图1,设:FC=4a,
∴cos∠ACB=![]() ,则EF=3a,EC=5a,
,则EF=3a,EC=5a,
∵∠EDC=∠α=∠CAD,∠ACD=∠ACD,
∴△ADC∽△DCE,
∴ACCE=CD2=DF2+FC2=36+16a2=105a,
解得:a=2或![]() (舍去a=2),
(舍去a=2),
AD=HF=10﹣2﹣4a=![]() ;
;
(2)过点C作CH⊥AD交AD的延长线于点H,
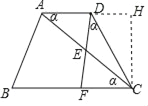
CD2=CH2+DH2=(ACsinα)2+(ACcosα﹣x)2,
即:CD2=36+(8﹣x)2,
由(1)得:ACCE=CD2,
即:y=![]() x2﹣
x2﹣![]() x+10(0<x≤10)…①,
x+10(0<x≤10)…①,
(3)①当DF=DC时,
∵∠ECF=∠FDC=α,∠DFC=∠DFC,
∴△DFC∽△CFE,∵DF=DC,
∴FC=EC=y,∴x+y=10,
即:10=![]() x2﹣
x2﹣![]() x+10+x,
x+10+x,
解得:x=6;
②当FC=DC,
则∠DFC=∠FDC=α,
则:EF=EC=y,DE=AE=10﹣y,
在等腰△ADE中,cos∠DAE=cosα= ,
,
即:5x+8y=80,
将上式代入①式并解得:x=![]() ;
;
③当FC=FD,
则∠FCD=∠FDC=α,而∠ECF=α≠∠FCD,不成立,
故:该情况不存在;
故:AD的长为6和![]() .
.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
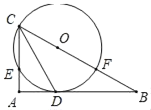
【题目】如图,Rt△ABC中,∠A=90°,CD平分∠ACB交AB于点D,O是BC上一点,经过C、D两点的⊙O分别交AC、BC于点E、F,AD=![]() ,∠ADC=60°,则劣弧
,∠ADC=60°,则劣弧![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
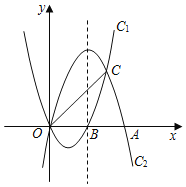
【题目】如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.
(1)在图1中画出一条长为![]() 的线段MN(M,N分别为格点)
的线段MN(M,N分别为格点)
(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;
(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项:评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了________名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为________度;
(3)请将频数分布直方图补充完整;
(4)如果全市有8600名七年级学生,那么在试卷评讲课中,“独立思考”的七年级学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:

(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数
128 000 000 000 000用科学计数法表示为( )
A. 1.28![]() 1014 B. 1.28
1014 B. 1.28![]() 10-14 C. 128
10-14 C. 128![]() 1012 D. 0.128
1012 D. 0.128![]() 1011
1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象相交于A,B两点(A在B的右侧).
)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若![]() ,求△ABC的面积.
,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为_____.
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com