
【题目】阅读下面材料:
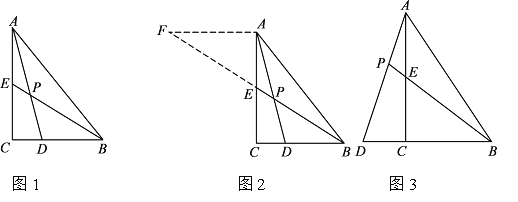
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
【答案】![]() 的值为
的值为![]() ;(1)
;(1)![]() ;(2) 6.
;(2) 6.
【解析】试题分析:易证△AEF≌△CEB,则有AF=BC.设CD=k,则DB=2k,AF=BC=3k,由AF∥BC可得△APF∽△DPB,然后根据相似三角形的性质就可求出![]() 的值;
的值;
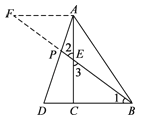
解决问题:(1)过点A作AF∥DB,交BE的延长线于点F,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.易证△AEF≌△CEB,则有EF=BE,AF=BC=2k.易证△AFP∽△DBP,然后根据相似三角形的性质就可求出![]() 的值;
的值;
(2)当CD=2时,可依次求出BC、AC、EC、EB、EF、BF的值,然后根据![]() 的值求出
的值求出![]() ,就可求出BP的值.
,就可求出BP的值.
试题解析:解:![]() 的值为
的值为![]() .
.
易证△AEF≌△CEB,则有AF=BC.
设CD=k,则DB=2k,AF=BC=3k,由AF∥BC可得△APF∽△DPB,即可得到![]() =
=![]() =
=![]() .故答案为:
.故答案为:![]() ;
;
解决问题:
(1)过点A作AF∥DB,交BE的延长线于点F,如图,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.∵E是AC中点,∴AE=CE.∵AF∥DB,∴∠F=∠1.
在△AEF和△CEB中,∵∠F=∠1,∠2=∠3,AE=CE,∴△AEF≌△CEB,∴EF=BE,AF=BC=2k.∵AF∥DB,∴△AFP∽△DBP,∴![]() =
=![]() ,∴
,∴![]() 的值为
的值为![]() ;
;
(2)当CD=2时,BC=4,AC=6,∴EC=![]() AC=3,EB=
AC=3,EB=![]() =5,∴EF=BE=5,BF=10.∵
=5,∴EF=BE=5,BF=10.∵![]() (已证),∴
(已证),∴![]() ,∴BP=
,∴BP=![]() BF=
BF=![]() ×10=6.
×10=6.
故答案为:6.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
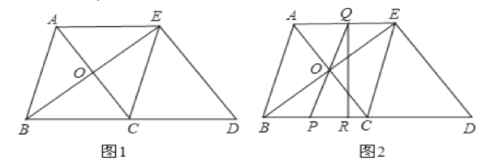
【题目】如图1,在△ABC中,AB=BC=5,AC=6,△ECD是△ABC沿BC方向平移得到的,连接AE、BE,且AC和BE相交于点O.
(1)求证:四边形ABCE是菱形;
(2)如图2,P是线段BC上一动点(不与B. C重合),连接PO并延长交线段AE于点Q,过Q作QR⊥BD交BD于R.
①四边形PQED的面积是否为定值?若是,请求出其值;若不是,请说明理由;
②以点P、Q、R为顶点的三角形与以点B. C. O为顶点的三角形是否可能相似?若可能,请求出线段BP的长;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司现有114吨货物,计划同时租出A,B两种型号的车,王经理发现一个运货货单上的一个信息是:
A型车(满载) | B型车(满载) | 运货总量 |
3辆 | 2辆 | 38吨 |
1辆 | 3辆 | 36吨 |
根据以上信息,解析下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)若物流公司打算一次运完,且恰好每辆车都装满货物,请你帮该物流公司设计租车方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】包装厂有工人42人,每个工人平均每小时可以生产圆形铁片120片,或长方形铁片80片,两张圆形铁片与一张长方形铁片可配套成一个密封圆桶,问每天如何安排工人生产圆形和长方形铁片能合理地将铁片配套?设安排x人生产圆形铁片,可以列方程:( )
A.120(42﹣x)=2×80xB.80(42﹣x)=120x
C.2×80(42﹣x)=120xD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:EF⊥AB;
(2)若∠C=30°,EF=![]() ,求EB的长.
,求EB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
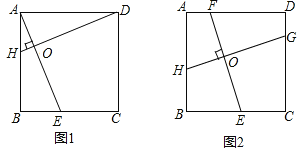
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形 ABCD ,有以下四个条件:① AB ∥ CD ;② BC ∥ AD ;③ AB CD ;④ABC ADC .从这四个条件中任选两个,能使四边形 ABCD 成为平行四边形的选法有( )
A.3 种B.4 种C.5 种D.6 种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形三个内角的度数之和是180°,如图是两个三角板不同位置的摆放,其中∠ACB=∠CDE=90°,∠BAC=60°,∠DEC=45°.
(1)当AB∥CD时,如图①,求∠DCB的度数;
(2)当CD与CB重合时,如图②,判断DE与AC的位置关系并说明理由;
(3)如图③,当∠DCB= 时,AB∥CE.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变量之间关系中,一个变量是另一个变量的正比例函数的是( )
A.正方形的面积S随着边长x的变化而变化
B.正方形的周长C随着边长x的变化而变化
C.水箱有水10升,以0.5升/分的流量往外放水,剩水量(升)随着放水时问t(分)的变化而变化
D.面积为20的三角形的一边a随着这边上的高h的变化而变化
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com