
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC,AO=DO,直线y=mx+1与y轴交于点D.
(1)求抛物线和直线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.

【答案】(1)y=﹣![]() x+1,y=x2﹣2x﹣3(2)证明见解析(3)P(1,﹣1)或P(1,
x+1,y=x2﹣2x﹣3(2)证明见解析(3)P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() )
)
【解析】分析:(1)抛物线![]() ,求出
,求出![]() 即可求得点
即可求得点![]() 的坐标,根据
的坐标,根据![]() ,求得点
,求得点![]() 的坐标,代入一次函数
的坐标,代入一次函数![]() 即可确定一次函数解析式,进而求得点
即可确定一次函数解析式,进而求得点![]() 的坐标,根据
的坐标,根据![]() 求得点
求得点![]() 的坐标,根据待定系数法即可确定二次函数解析式.
的坐标,根据待定系数法即可确定二次函数解析式.
(2)先把抛物线解析式配成顶点式得到E(1,-4),再利用一次函数解析式确定D(0,1),则利用两点间的距离公式可计算出![]()
![]()
![]() 而得到
而得到![]() 然后根据相似三角形的判定方法可判断
然后根据相似三角形的判定方法可判断![]()
(3)设设P(1,m),则利用两点间的距离公式可得![]()
![]()
![]() 然后分类讨论即可.
然后分类讨论即可.
详解:(1)∵抛物线![]() ,
,![]()
∴![]()
∵![]()
![]()
把![]() 代入
代入![]() 得
得![]()
∴直线解析式为![]() ,
,
∵直线![]() 与y轴交于点D,
与y轴交于点D,![]()
∵![]()
![]()
∵该抛物线与x轴交于A、B两点,
![]() 解得:
解得:![]()
∴抛物线解析式为![]()
(2)证明:∵
![]()
∴E(1,4),
当x=0时, ![]() ,则D(0,1),
,则D(0,1),
∵B(3,0),A(1,0),C(0,3),
∴![]()
![]()
∵![]()
∴![]()
∴△BCE∽△BDO;
(3)存在,
理由:抛物线的对称轴为直线x=1,设P(1,m),则![]()
当PB=PC时,△PBC是等腰三角形,则m2+4=(m+3)2+1,解得m=1,此时P(1,1),
当PB=BC时,△PBC是等腰三角形,则m2+4=18,解得![]() 此时
此时![]() 或
或![]()
当PC=BC时,△PBC是等腰三角形,则(m+3)2+1=18,解得![]() 此时
此时![]() 或
或![]()
综上所述,当符P点坐标为(1,1)或![]() 或
或![]() 或
或![]() 或
或![]() 时,△PBC是等腰三角形。
时,△PBC是等腰三角形。


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形OABC的两个顶点A、B的坐标分别![]()

(1)求对角线AC所在的直线的函数表达式;
(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;
(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
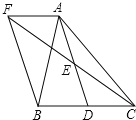
【题目】如图,在![]() 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且
中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且![]() ,连接BF.
,连接BF.
![]() 证明:
证明:![]() ;
;
![]() 当
当![]() 满足什么条件时,四边形AFBD是矩形?并说明理由.
满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (a是常数,a≠0),下列结论正确的是( )
(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象经过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a<0,函数图象的顶点始终在x轴的下方
D.若a>0,则当x≥1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,已知直线![]() 经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB
经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB
(1)求直线![]() 的函数解析式
的函数解析式
(2)若直线![]() 也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标
也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)将最后一名老师送到目的地时,小王距出发地多少千米?
(2)若汽车耗油量为0.5升/千米,则当天耗油多少升?若汽油价格为6.70元/升,则小王共花费了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国汉字听写大会》唤醒了很多人对文字基本功的重视和对汉字文化的学习,我市某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:

请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
(4)经过统计发现,在E组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=12,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM?
(2)当P在线段AB上运动时,试说明2BM﹣BP为定值.
(3)当P在AB延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变,选择一个正确的结论,并求出其值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com