
分析 根据整式、单项式、多项式的定义,进行分类即可.
解答 解:代数式:-$\frac{1}{3}$,$\frac{3}{a}$,-π,-5x2y2$•\frac{2x{y}^{2}}{3}$$•\frac{a+b}{2}$,$\frac{1}{2}-x$,$\frac{5}{x+3}$,其中属于单项式的有-$\frac{1}{3}$,-π;属于多项式的有-5x2y2$•\frac{2x{y}^{2}}{3}$$•\frac{a+b}{2}$,$\frac{1}{2}-x$;属于整式的有-$\frac{1}{3}$,-π,-5x2y2$•\frac{2x{y}^{2}}{3}$$•\frac{a+b}{2}$,$\frac{1}{2}-x$.
故答案为:-$\frac{1}{3}$,-π;-5x2y2$•\frac{2x{y}^{2}}{3}$$•\frac{a+b}{2}$,$\frac{1}{2}-x$;-$\frac{1}{3}$,-π,-5x2y2$•\frac{2x{y}^{2}}{3}$$•\frac{a+b}{2}$,$\frac{1}{2}-x$
点评 本题考查了多项式、整式及单项式的知识,解答本题的关键是掌握三者的定义.


科目:初中数学 来源: 题型:选择题
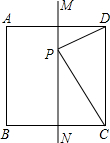 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a的系数为0 | B. | ab2c的次数是2 | ||
| C. | $\frac{1}{2}$πxy3的系数为$\frac{1}{2}$π | D. | -5是一次单项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
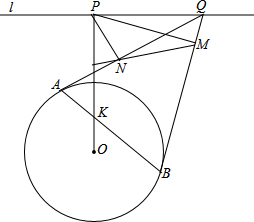 如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.
如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com