
【题目】已知二次函数y=﹣x2+bx+c+1。
(1)当b=1时,求这个二次函数的对称轴的方程;
(2)若c=﹣![]() b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
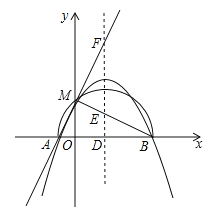
(3)若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,b>0,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足![]() =
=![]() ,求二次函数的表达式.
,求二次函数的表达式.
【答案】(1)对称轴的方程为x=![]() ;(2)b=
;(2)b=![]() ;(3)y=﹣x2+
;(3)y=﹣x2+![]() x+1.
x+1.
【解析】试题分析:(1)二次函数y=﹣x2+bx+c+1的对称轴为x=![]() ,即可得出答案;
,即可得出答案;
(2)二次函数y=﹣x2+bx+c+1的顶点坐标为(![]() ),y由二次函数的图象与x轴相切且c=
),y由二次函数的图象与x轴相切且c=![]() b2﹣2b,得出方程组
b2﹣2b,得出方程组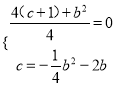 ,求出b即可;
,求出b即可;
(3)由圆周角定理得出∠AMB=90°,证出∠OMA=∠OBM,得出△OAM∽△OMB,得出OM2=OAOB,由二次函数的图象与x轴的交点和根与系数关系得出OA=﹣x1,OB=x2,x1+x2=b,x1x2=﹣(c+1),得出方程(c+1)2=c+1,得出c=0,OM=1,证明△BDE∽△BOM,△AOM∽△ADF,得出![]() ,得出OB=4OA,即x2=﹣4x1,由x1x2=﹣(c+1)=﹣1,得出方程组
,得出OB=4OA,即x2=﹣4x1,由x1x2=﹣(c+1)=﹣1,得出方程组![]() ,解方程组求出b的值即可.
,解方程组求出b的值即可.
试题解析:解:(1)二次函数y=﹣x2+bx+c+1的对称轴为x=![]() ,当b=1时,
,当b=1时, ![]() =
=![]() ,∴当b=1时,这个二次函数的对称轴的方程为x=
,∴当b=1时,这个二次函数的对称轴的方程为x=![]() .
.
(2)二次函数y=﹣x2+bx+c+1的顶点坐标为(![]() ).∵二次函数的图象与x轴相切且c=﹣
).∵二次函数的图象与x轴相切且c=﹣![]() b2﹣2b,∴
b2﹣2b,∴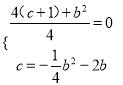 ,
,![]() ,∴b为
,∴b为![]() ,二次函数的图象与x轴相切.
,二次函数的图象与x轴相切.
(3)∵AB是半圆的直径,∴∠AMB=90°,∴∠OAM+∠OBM=90°.∵∠AOM=∠MOB=90°,∴∠OAM+∠OMA=90°,∴∠OMA=∠OBM,∴△OAM∽△OMB,∴![]() ,∴OM2=OAOB.∵二次函数的图象与x轴交于点A(x1,0),B(x2,0),∴OA=﹣x1,OB=x2,x1+x2=b,x1x2=﹣(c+1).∵OM=c+1,∴(c+1)2=c+1,解得:c=0或c=﹣1(舍去),∴c=0,OM=1.∵二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足
,∴OM2=OAOB.∵二次函数的图象与x轴交于点A(x1,0),B(x2,0),∴OA=﹣x1,OB=x2,x1+x2=b,x1x2=﹣(c+1).∵OM=c+1,∴(c+1)2=c+1,解得:c=0或c=﹣1(舍去),∴c=0,OM=1.∵二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足![]() =
=![]() ,∴AD=BD,DF=4DE,DF∥OM,∴△BDE∽△BOM,△AOM∽△ADF,∴
,∴AD=BD,DF=4DE,DF∥OM,∴△BDE∽△BOM,△AOM∽△ADF,∴![]() ,∴DE=
,∴DE=![]() ,DF=
,DF=![]() ,∴
,∴![]() ×4,∴OB=4OA,即x2=﹣4x1.∵x1x2=﹣(c+1)=﹣1,∴
×4,∴OB=4OA,即x2=﹣4x1.∵x1x2=﹣(c+1)=﹣1,∴![]() ,解得:
,解得: 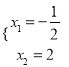 ,∴b=﹣
,∴b=﹣![]() +2=
+2=![]() ,∴二次函数的表达式为y=﹣x2+
,∴二次函数的表达式为y=﹣x2+![]() x+1.
x+1.


科目:初中数学 来源: 题型:
【题目】已知在数轴上,一动点![]() 从原点
从原点![]() 出发,沿直线以每秒钟
出发,沿直线以每秒钟![]() 个单位长度的速度来回移动,其移动方式是先向右移动
个单位长度的速度来回移动,其移动方式是先向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度…
个单位长度…
![]()
(1)求出![]() 秒钟后动点
秒钟后动点![]() 所处的位置;
所处的位置;
(2)如果在数轴上还有一个定点![]() ,且
,且![]() 与原点
与原点![]() 相距20个单位长度,问:动点
相距20个单位长度,问:动点![]() 从原点出发,可能与点
从原点出发,可能与点![]() 重合吗?若能,则第一次与点
重合吗?若能,则第一次与点![]() 重合需多长时间?若不能,请说明理由.
重合需多长时间?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.
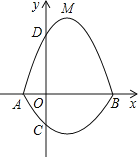
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣1,点B表示的数为3,点P为数轴上一动点.
(1)点A到原点O的距离为 个单位长度;点B到原点O的距离为 个单位长度;线段AB的长度为 个单位长度;
(2)若点P到点A、点B的距离相等,则点P表示的数为 ;
(3)数轴上是否存在点P,使得PA+PB的和为6个单位长度?若存在,请求出PA的长;若不存在,请说明理由?
(4)点P从点A出发,以每分钟1个单位长度的速度向左运动,同时点Q从点B出发,以每分钟2个单位长度的速度向左运动,请直接回答:几分钟后点P与点Q重合?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数6,
点表示数6,
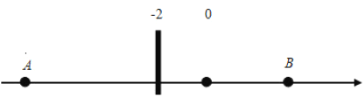
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点![]() ,它表示的数是
,它表示的数是![]() ,则
,则![]() 的最小值是_________;
的最小值是_________;
(3)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数是_________;
点表示的数是_________;
(4)若在原点![]() 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点![]() 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点![]() 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为![]() 秒,请用
秒,请用![]() 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
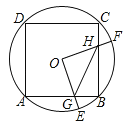
【题目】(2016湖北省咸宁市)如图,边长为4的正方形ABCD内接于点O,点E是![]() 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是![]() 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
①![]() ;
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为![]() .
.
其中正确的是________(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
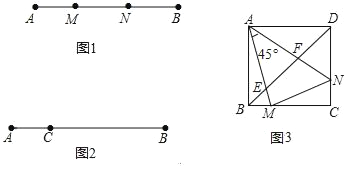
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可);
(3)如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F.
求证:①E、F是线段BD的勾股分割点;
②△AMN的面积是△AEF面积的两倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种型号的台灯1000台,这两种型号台灯的进价、售价如下表:
进价(元/台) | 售价(元/台) | |
甲种 | 45 | 55 |
乙种 | 60 | 80 |
(1)如果超市的进货款为54000元,那么可计划购进甲、乙两种型号的台灯各多少台?
(2)为确保乙种型号的台灯销售更快,超市决定对乙种型号的台灯打折销售,且保证乙种型号台灯的利润率为![]() ,问乙种型号台灯需打几折?
,问乙种型号台灯需打几折?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com