
| A. | 当a=1时,函数图象过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a>0,则当x≥1时,y随x的增大而减小 | |
| D. | 不论a为何值,函数图象必经过(2,-1) |
分析 将a=1,x=-1代入可判断A;将a=-2代入函数再求△可判断B;根据函数图象的对称轴及增减性可判断C;把x=2代入可判断D.
解答 解:a=1,x=-1时,y=1-2×(-1)-1=2,所以A错误;
当a=-2时,y=-2x2-4x-1,△=(-4)2-4×(-2)×(-1)=8>0,与x轴有两个交点,所以B错误;
对称轴x=$-\frac{-2a}{2×a}$=1,a>0,所以则当x≥1时,y随x的增大而增大,所以C错误;
当x=2时,y=4a-4a-1=-1,所以D正确,
故选D.
点评 本题主要考查了二次函数根与系数的关系,关键是熟练掌握以下知识点:
二次函数y=ax2+bx+c(a≠0)
①二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;IaI还可以决定开口大小,IaI越大开口就越小.
②一次项系数b和二次项系数a共同决定对称轴的位置. 当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)
③.常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


科目:初中数学 来源: 题型:填空题
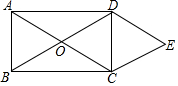 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,下列结论:①AB=2;②∠E=45°;③四边形OCED是菱形;④四边形OCED的面积为2$\sqrt{3}$,其中正确的是①③④(把所有正确结论的序号都填上).
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,下列结论:①AB=2;②∠E=45°;③四边形OCED是菱形;④四边形OCED的面积为2$\sqrt{3}$,其中正确的是①③④(把所有正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y<0 | B. | 0<y<m | C. | m<y<m+4 | D. | y>m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
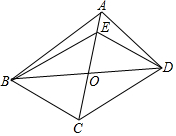 如图,在四边形ABCD中,对角线AC、BD相交于点O,且OB=OD,点E在线段OA上,连接BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是①②(只填写序号).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且OB=OD,点E在线段OA上,连接BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是①②(只填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
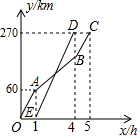 小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
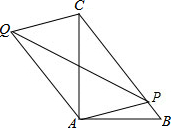 如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$.
如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
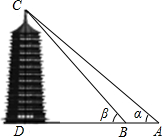 一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米.
一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com