
【题目】某服装网店李经理用11000元购进了甲、乙两种款式的童装共150套,两种童装的进价如下图所示:

(1)请你求出李经理购买甲、乙两种款式的童装各多少套?
(2)根据销售状况,李经理计划再购进甲、乙两种款式的童装共100套,若进价不变,费用不超过8000元,求至少需要购进甲种款式的童装多少套?
【答案】(1)李经理购买甲种款式的童装70套,购买乙种款式的童装80套;(2)李经理至少需要购进甲种款式的童装20套.
【解析】
(1)设甲种款式的童装x件,乙种款式的童装y件,根据“用11000元购进了甲、乙两种款式的童装共150套”列出方程组,解答即可;
(2)设李经理购买甲种款式的童装![]() 套,根据“100套的总费用不超过8000元”列出不等式,求解即可.
套,根据“100套的总费用不超过8000元”列出不等式,求解即可.
解:(1)设李经理购买甲种款式的童装![]() 套,购买乙种款式的童装
套,购买乙种款式的童装![]() 套.
套.
根据题意,列方程得
![]()
解方程,得![]()
答:李经理购买甲种款式的童装70套,购买乙种款式的童装80套.
(2)设李经理购买甲种款式的童装![]() 套.
套.
根据题意,得![]()
解得![]()
答:李经理至少需要购进甲种款式的童装20套.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有射线AP和点B,C,请用尺规按下列要求作图:
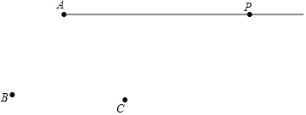
(1)连接AB,并在射线AP上截取AD=AB;
(2)连接BC、BD,并延长BC到E,使BE=BD.
(3)在(2)的基础上,取BE中点F,若BD=6,BC=4,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年9月1日,长春首届航空开放日在长春大房身机场正式举行,空军八一飞行表演队的新换装歼-10飞机,进行了精彩的特技飞行表演,其中一架飞机起飞0.5千米后的高度变化如下表:
高度变化 | 上升4.2 | 下降3.5 | 上升1.4 | 下降1.2 |
记作 | +4.2 | -3.5 | +1.4 | -1.2 |
(1)此时这架飞机飞离地面的高度是多少千米?
(2)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.6干米,下降2.8千米,再上升1.5千米,最后下降0.9千米.若飞机平均上升1干米需消耗6升燃油,平均下降1千米需消耗4升燃油,那么这架飞机在这4个特技表演过程中,一共消耗了多少升燃油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的周长为12,E,F,G,H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.
(1)请直接写出y与x之间的函数关系式;
(2)根据(1)中的函数关系式,计算当x为何值时,y最大,并求出最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理
表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理![]() 也可理解为
也可理解为![]() 与3两数在数轴上所对应的两点之间的距离,
与3两数在数轴上所对应的两点之间的距离,![]() 就表示
就表示![]() 在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求![]() .
.
(2)若![]() ,则
,则![]() .
.
(3)请你找出所有符合条件的整数![]() ,使得
,使得![]() .
.
(4)求![]() 的最小值,并写出此时
的最小值,并写出此时![]() 的取值情况.
的取值情况.
(5)已知![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )

A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是线段AB的中点,Q为线段PB上一点,分别以AQ、AP、PQ、QB为一边作正方形,其面积对应地记作SACDQ,SAEFP,SPGHQ,SQIJB,设AP=m,QB=n,
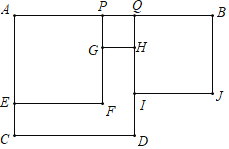
(1)用含有m,n的代数式表示正方形ACDQ的面积SACDQ.
(2)SACDQ+SQIJB与SAEFP+SPGHQ具有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=4∠DOE,∠COE=α,则∠BOE的度数为___________.(用含α的式子表示)
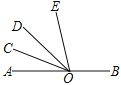
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com