
【题目】如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果![]() ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和![]() 的值.
的值.

【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)∠CDF的度数为45°,
,证明见解析;(3)∠CDF的度数为45°,![]() 的值为
的值为![]() .
.
【解析】(1)先证明△CDA是等腰三角形,再根据等腰三角形的性质证明AM+CK=MK;在△MKD中,AM+CK>MK(两边之和大于第三边);
(2)作点C关于FD的对称点G,连接GK,GM,GD.证明△ADM≌△GDM后,根据全等三角形的性质,GM=AM,GM+GK>MK,∴AM+CK>MK;
(3)根据勾股定理的逆定理求得∠GKM=90°,又∵点C关于FD的对称点G,∴<CKG=90°,<FKC=![]() <CKG=45°,根据三角形的外角定理,就可以求得∠CDF=15°;在Rt△GKM中,∠MGK=∠DGK+∠MGD=∠A+∠ACD=60°,∴∠GMK=30°,利用余弦定理解得
<CKG=45°,根据三角形的外角定理,就可以求得∠CDF=15°;在Rt△GKM中,∠MGK=∠DGK+∠MGD=∠A+∠ACD=60°,∴∠GMK=30°,利用余弦定理解得![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知:一次函数的表达式为y=![]() x﹣1
x﹣1
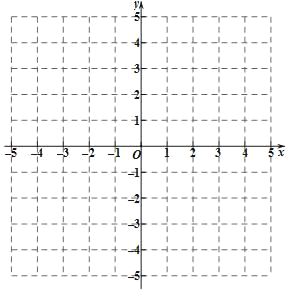
(1)该函数与x轴交点坐标为 ,与y轴的交点坐标为 ;
(2)画出该函数的图象(不必列表);
(3)根据该函数的图象回答下列问题:
①当x 时,则y>0;
②当﹣2≤x<4时,则y的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年宜宾市创建全国文明城市的过程中,某小区决定购买文明用语提示牌和文明信息公示栏.若购买2个提示牌和3个公示栏需要510元;购买3个提示牌和5个公示栏需要840元.
(1)求提示牌和公示栏的单价各是多少元?
(2)若该小区购买提示牌和公示栏共50个,要求购买公示栏至少12个,且总费用不超过3200元.请你列举出所有购买方案,并指出哪种方案费用最少,最少费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.
(1)试判断△PMN的形状,并证明你的结论;
(2)若CD=5,AC=12,求△PMN的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以点A为顶点作等腰Rt△ABC,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE,延长BD交CE于点F.

(1)试判断BD、CE的关系,并说明理由;
(2)把两个等腰直角三角形按如图2所示放置,(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的![]() ,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的( )
,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在下面平面直角坐标系中,已知A ![]() ,B
,B ![]() ,C
,C ![]() 三点.其中
三点.其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)如果在第二象限内有一点![]()
![]() ,请用含
,请用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(3)在(2)的条件下,是否存在点![]() ,使四边形
,使四边形![]() 的面积为△
的面积为△![]() 的面积的两倍?若存在,求出点
的面积的两倍?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低![]() 元,则每天的销售量是__________斤(用含
元,则每天的销售量是__________斤(用含![]() 的代数式表示);
的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com