
分析 因为B(0,m),C(2,m)在二次函数y=a(x-h)2+k(a,h,k为常数,且a≠0)的图象上,所以抛物线的对称轴x=1,可得二次函数的解析式为y=a(x-1)2+k,把(A(-1,0)代入可得k=-4a,所以方程ax2+k=0即为方程ax2-4a=0,由此即可解决问题.
解答 解:∵B(0,m),C(2,m)在二次函数y=a(x-h)2+k(a,h,k为常数,且a≠0)的图象上,
∴抛物线的对称轴x=1,
∴二次函数的解析式为y=a(x-1)2+k,把(A(-1,0)代入可得k=-4a,
∴方程ax2+k=0为方程ax2-4a=0,
∵a≠0,
∴x=±2,
故答案为±2
点评 本题考查抛物线与x轴的交点问题、二次函数图象上的点的坐标特征,解题的关键是确定抛物线的对称轴x=1,灵活运用待定系数法解决问题,所以中考填空题中的压轴题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:解答题
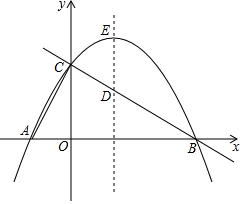 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{3}$x2+$\frac{2\sqrt{3}}{3}$x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{3}$x2+$\frac{2\sqrt{3}}{3}$x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
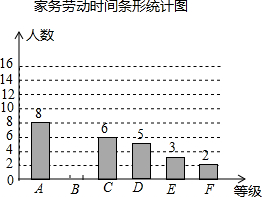 某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:
某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:| 等级 | 家务劳动时间 (分钟) | 人数 | 百分比 |
| A | 50以上 | 8 | 20% |
| B | 41-50 | a | 40% |
| C | 31-40 | 6 | 15% |
| D | 21-30 | 5 | 12.5% |
| E | 11-20 | 3 | 7.5% |
| F | 0-10 | 2 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com