
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
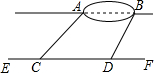 某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.
某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com