
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy£½£![]() x+4ÓėxÖį½»ÓŚµćA£¬Óėy½»ÓŚµćC£¬ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼Ļó¾¹żµćA£¬CŗĶµćB£Ø£1£¬0£©£¬
x+4ÓėxÖį½»ÓŚµćA£¬Óėy½»ÓŚµćC£¬ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼Ļó¾¹żµćA£¬CŗĶµćB£Ø£1£¬0£©£¬
£Ø1£©Ēóøƶž“ĪŗÆŹżµÄ¹ŲĻµŹ½£»
£Ø2£©Éčøƶž“ĪŗÆŹżµÄĶ¼ĻóµÄ¶„µćĪŖM£¬ĒóĖıߊĪAOCMµÄĆ껿£»
£Ø3£©ÓŠĮ½øö¶ÆµćD”¢EĶ¬Ź±“ÓµćO³ö·¢£¬ĘäÖŠµćDŅŌĆæĆė![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÕŪĻßOAC°“O”śA”śCµÄĀ·ĻßŌĖ¶Æ£¬µćEŅŌĆæĆė4øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÕŪĻßOCA°“O”śC”śAµÄĀ·ĻßŌĖ¶Æ£¬µ±µćD”¢EĮ½µćĻąÓöŹ±£¬ĖüĆĒ¶¼Ķ£Ö¹ŌĖ¶Æ£¬ÉčD£¬EĶ¬Ź±“ÓµćO³ö·¢tĆėŹ±£¬”÷ODEµÄĆ껿ĪŖS£¬
øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÕŪĻßOAC°“O”śA”śCµÄĀ·ĻßŌĖ¶Æ£¬µćEŅŌĆæĆė4øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÕŪĻßOCA°“O”śC”śAµÄĀ·ĻßŌĖ¶Æ£¬µ±µćD”¢EĮ½µćĻąÓöŹ±£¬ĖüĆĒ¶¼Ķ£Ö¹ŌĖ¶Æ£¬ÉčD£¬EĶ¬Ź±“ÓµćO³ö·¢tĆėŹ±£¬”÷ODEµÄĆ껿ĪŖS£¬

¢ŁĒėĪŹD£¬EĮ½µćŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚDE”ĪOC£¬Čō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±tµÄÖµ£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
¢ŚÖ±½ÓŠ“³öS¹ŲÓŚtµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮætµÄȔֵ·¶Ī§£»
¢ŪŌŚ¢ŚÖŠ£¬µ±tŹĒ¶ąÉŁŹ±£¬SÓŠ×ī“óÖµ£¬²¢Ēó³öÕāøö×ī“óÖµ.
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©10£Ø3£©¢Ł²»“ęŌŚDE”ĪOC¢Śµ±0£¼t”Ü1Ź±£¬S£½3t2£»µ±1£¼t”Ü2Ź±£¬S£½
£»£Ø2£©10£Ø3£©¢Ł²»“ęŌŚDE”ĪOC¢Śµ±0£¼t”Ü1Ź±£¬S£½3t2£»µ±1£¼t”Ü2Ź±£¬S£½![]() £»µ±2£¼t”Ü
£»µ±2£¼t”Ü![]() Ź±£¬S£½£
Ź±£¬S£½£![]() £»¢Ūµ±t£½
£»¢Ūµ±t£½![]() Ź±£¬SÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ
Ź±£¬SÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ![]() .
.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ĻČøł¾ŻÖ±ĻßACµÄ½āĪöŹ½Ēó³öA”¢CĮ½µćµÄ×ų±ź£¬Č»ŗóøł¾ŻA”¢B”¢CČżµćµÄ×ų±źÓĆ“ż¶ØĻµŹż·Ø¼“æÉĒó³öÅ×ĪļĻߵĽāĪöŹ½£®
£Ø2£©øł¾ŻÅ×ĪļĻߵĽāĪöŹ½æÉĒó³öMµćµÄ×ų±ź£¬ÓÉÓŚĖıߊĪOAMC²»ŹĒ¹ęŌņµÄĖıߊĪ£¬Ņņ“ĖæɹżM×÷xÖįµÄ“¹Ļߣ¬½«ĖıߊĪOAMC·Ö³ÉŅ»øöÖ±½ĒČż½ĒŠĪŗĶŅ»øöÖ±½ĒĢŻŠĪĄ“Ēó½ā£®
£Ø3£©¢ŁČē¹ūDE”ĪOC£¬“ĖŹ±µćD£¬EÓ¦·Ö±šŌŚĻ߶ĪOA£¬CAÉĻ£¬ĻČĒó³öÕāøöĒų¼ätµÄȔֵ·¶Ī§£¬Č»ŗóøł¾ŻĘ½ŠŠĻß·ÖĻ߶Ī³É±ČĄż¶ØĄķ£¬Ēó³ö“ĖŹ±tµÄÖµ£¬Č»ŗóæ“tµÄÖµŹĒ·ń·ūŗĻ“ĖÖÖĒéæöĻĀtµÄȔֵ·¶Ī§£®Čē¹ū·ūŗĻŌņÕāøötµÄÖµ¾ĶŹĒĖłĒóµÄÖµ£¬Čē¹ū²»·ūŗĻ£¬ÄĒĆ“¾ĶĖµĆ÷²»“ęŌŚÕāŃłµÄt£®
¢Ś±¾ĢāŅŖ·ÖČżÖÖĒéæö½ųŠŠĢÖĀŪ£ŗ
µ±EŌŚOCÉĻ£¬DŌŚOAÉĻ£¬¼“µ±0£¼t”Ü1Ź±£¬“ĖŹ±S=![]() OEOD£¬ÓÉ“ĖæÉµĆ³ö¹ŲÓŚS£¬tµÄŗÆŹż¹ŲĻµŹ½£»
OEOD£¬ÓÉ“ĖæÉµĆ³ö¹ŲÓŚS£¬tµÄŗÆŹż¹ŲĻµŹ½£»
µ±EŌŚACÉĻ£¬DŌŚOAÉĻ£¬¼“µ±1£¼t”Ü2Ź±£¬“ĖŹ±S=![]() OD”ĮEµćµÄׯ×ų±ź£®ÓÉ“ĖæÉµĆ³ö¹ŲÓŚS£¬tµÄŗÆŹż¹ŲĻµŹ½£»
OD”ĮEµćµÄׯ×ų±ź£®ÓÉ“ĖæÉµĆ³ö¹ŲÓŚS£¬tµÄŗÆŹż¹ŲĻµŹ½£»
µ±E£¬D¶¼ŌŚCAÉĻŹ±£¬¼“µ±2£¼t£¼![]() ĻąÓöŹ±ÓƵď±¼ä£¬“ĖŹ±S=S”÷AOE-S”÷AOD£¬ÓÉ“ĖæÉµĆ³öS£¬tµÄŗÆŹż¹ŲĻµŹ½£»
ĻąÓöŹ±ÓƵď±¼ä£¬“ĖŹ±S=S”÷AOE-S”÷AOD£¬ÓÉ“ĖæÉµĆ³öS£¬tµÄŗÆŹż¹ŲĻµŹ½£»
×ŪÉĻĖłŹö£¬æÉµĆ³ö²»Ķ¬µÄtµÄȔֵ·¶Ī§ÄŚ£¬ŗÆŹżµÄ²»Ķ¬±ķ“ļŹ½£®
¢Ūøł¾Ż¢ŚµÄŗÆŹż¼“æÉµĆ³öSµÄ×ī“óÖµ£®
ŹŌĢā½āĪö£ŗ£Ø1£©¶ŌÓŚŅ»“ĪŗÆŹży£½£![]() x+4£¬µ±x£½0Ź±£¬y£½4£¬µ±y£½0Ź±£¬x£½3£¬
x+4£¬µ±x£½0Ź±£¬y£½4£¬µ±y£½0Ź±£¬x£½3£¬
”ąA£Ø3£¬0£©£¬C£Ø0£¬4£©£¬
É趞“ĪŗÆŹż¹ŲĻµŹ½ĪŖy£½ax2+bx+c£¬
°ŃA£Ø3£¬0£©£¬C£Ø0£¬4£©£¬B£Ø£1£¬0£©“śČėµĆ£ŗ
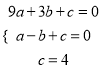 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ 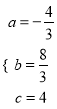 £¬
£¬
”ą¶ž“ĪŗÆŹżµÄ¹ŲĻµŹ½ĪŖ![]() £»
£»
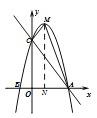
£Ø2£©ÓÉ![]() µĆ£ŗ
µĆ£ŗ ![]()
”ąÅ×ĪļĻߵĶ„µćMµÄ×ų±źĪŖ£Ø1£¬ ![]() £©£¬
£©£¬
¹żµćM×÷MN”ĶxÖįÓŚµćN£¬ŌņON£½1£¬MN£½![]() £¬
£¬
”ßA£Ø3£¬0£©£¬C£Ø0£¬4£©£¬
”ąOC£½4£¬AN£½3£1£½2£¬
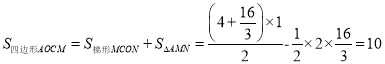
“š£ŗĖıߊĪAOCNµÄĆ껿ĪŖ10
£Ø3£©¢Ł²»“ęŌŚDE”ĪOC£¬
¼ŁÉčDE”ĪOC£¬ŌņDŌŚOAÉĻ£¬EŌŚACÉĻ£¬ĒŅ1£¼t£¼2£¬
“ĖŹ±£¬OD£½![]() £¬AD£½3£
£¬AD£½3£![]() £¬CE£½4t£4£¬AE£½9£4t£¬
£¬CE£½4t£4£¬AE£½9£4t£¬
”ßDE”ĪOC£¬”ą ![]() £¬¼“
£¬¼“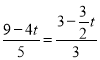 £¬
£¬
½āµĆ£ŗt£½![]()
”ßt£½![]() £¾2£¬”ą²»“ęŌŚDE”ĪOC£¬
£¾2£¬”ą²»“ęŌŚDE”ĪOC£¬
¢Śµ±0£¼t”Ü1Ź±£¬S£½3t2£»
µ±1£¼t”Ü2Ź±£¬S£½![]() £»
£»
µ±2£¼t”Ü![]() Ź±£¬S£½£
Ź±£¬S£½£![]() £»
£»
¢ŪÓÉS£½![]() £¬µĆ£ŗS£½
£¬µĆ£ŗS£½![]() £¬
£¬
”ß![]() £¼0£¬
£¼0£¬
”ąµ±t£½![]() Ź±£¬SÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ
Ź±£¬SÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ![]() .
.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōµćM£Øk©1£¬k+1£©¹ŲÓŚyÖįµÄ¶Ō³ĘµćŌŚµŚĖÄĻóĻŽÄŚ£¬ŌņŅ»“ĪŗÆŹży=£Øk©1£©x+kµÄĶ¼Ļó²»¾¹żµŚĻóĻŽ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŌŚRt”÷ABCÖŠ£¬AB=AC=2£¬ŌŚ”÷ABCÄŚ×÷µŚŅ»øöÄŚ½ÓÕż·½ŠĪDEFG£»Č»ŗóČ”GFµÄÖŠµćP£¬Į¬½ÓPD”¢PE£¬ŌŚ”÷PDEÄŚ×÷µŚ¶žøöÄŚ½ÓÕż·½ŠĪHIKJ£»ŌŁČ”Ļ߶ĪKJµÄÖŠµćQ£¬ŌŚ”÷QHIÄŚ×÷µŚČżøöÄŚ½ÓÕż·½ŠĪ”ŅĄ“Ī½ųŠŠĻĀČ„£¬ŌņµŚnøöÄŚ½ÓÕż·½ŠĪµÄ±ß³¤ĪŖ£Ø””””£©

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻ£ĶūŠ”ѧѧɜĶõ¾§ŗĶĖūµÄ°Ö°Ö”¢ĀčĀč×¼±øŌŚ”°ŌŖµ©”±ĘŚ¼äĶā³öĀĆÓĪ£®Ńō¹āĀĆŠŠÉēµÄŹÕ·Ń±ź×¼ĪŖ£ŗ“óČĖČ«¼Ū£¬Š”ŗ¢°ė¼Ū£»¶ųĄ¶ĢģĀĆŠŠÉē²»¹Ü“óČĖŠ”ŗ¢£¬Ņ»ĀÉ°ĖÕŪ£®ÕāĮ½¼ŅĀĆŠŠÉēµÄ»ł±¾·ŃŅ»Ńł£¬¶¼ŹĒ300ŌŖ£¬ÄćČĻĪŖÓ¦øĆČ„ÄļŅĀĆŠŠÉē½ĻĪŖŗĻĖć£æĪŖŹ²Ć“£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻB=90”ć£¬AC=120cm£¬”ĻA=60”ć£¬µćD“ÓµćC³ö·¢ŃŲ CA·½ĻņŅŌ4cm/ĆėµÄĖŁ¶ČĻņµćAŌČĖŁŌĖ¶Æ£¬Ķ¬Ź±µćE“ÓµćA³ö·¢ŃŲAB·½ĻņŅŌ2cm/ĆėµÄĖŁ¶ČĻņµćBŌČĖŁŌĖ¶Æ£¬µ±ĘäÖŠŅ»øöµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®ÉčµćD”¢EŌĖ¶ÆµÄŹ±¼äŹĒtĆė£®¹żµćD×÷DF”ĶBCÓŚµćF£¬Į¬½ÓDE£¬EF£®µ±ĖıߊĪAEFDŹĒĮāŠĪŹ±£¬tµÄÖµĪŖ£Ø £©
A.20Ćė
B.18Ćė
C.12Ćė
D.6Ćė
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōx=0ŹĒ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģ£Øm©2£©x2+3x+m2+2m©8=0µÄŅ»øö½ā£¬Ē󏵏żmµÄÖµŗĶĮķŅ»øöøł£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹Ū²ģĻĀĮŠµ„ĻīŹ½£ŗ-2x£¬22x2£¬-23x3£¬24x4”-25x5£¬26x6”Ēė¹Ū²ģ¹ęĀÉ£¬Š“³öµŚnøöŹ½×Ó________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æøų³öŅ»ÖÖŌĖĖć£ŗ¶ŌÓŚŗÆŹży£½xn£¬¹ę¶Øy'£½n”Įxn©1£®ČōŗÆŹży£½x4£¬ŌņÓŠy'£½4”Įx3£¬ŅŃÖŖŗÆŹży£½x3£¬Ōņ·½³Ģy'£½6xµÄ½āŹĒ£Ø””””£©
A. x£½2B. x£½3C. x1£½0£¬x2£½2D. x£½©2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĖµ·ØÕżČ·µÄŹĒ( )
A. ÓŠŅ»×é¶Ō½ĒŹĒÖ±½ĒµÄĖıߊĪŅ»¶ØŹĒ¾ŲŠĪ B. ÓŠŅ»×éĮŚ½ĒŹĒÖ±½ĒµÄĖıߊĪŅ»¶ØŹĒ¾ŲŠĪ
C. ¶Ō½ĒĻß»„ĻąĘ½·ÖµÄĖıߊĪŹĒ¾ŲŠĪ D. ¶Ō½Ē»„²¹µÄĘ½ŠŠĖıߊĪŹĒ¾ŲŠĪ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com