练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    (6分)
    如图，在边长为1的小正方形组成的网格中，△ABC的顶点均在格点上，以直线BC为对称轴作△ABC的轴对称图形，得到△A1BC，再将△A1BC绕着点B逆时针旋转90°，得到△A2BC1 ，请依此画出△A1BC，、△A2BC1

    略

    解析考点：作图-旋转变换；作图-轴对称变换．
    专题：作图题．
    分析：根据对称轴垂直平分对应点连线可得出各点的对称点，从而顺次连接可得出△A1BC，然后根据旋转角度为90°，旋转方向为逆时针及旋转中心为点B可得出各点的对应点，顺次连接可得出△A2BC1．
    解答：解：对称轴垂直平分对应点连线可得出各点的对称点，所作图形如下：

    根据旋转角度为90°，旋转方向为逆时针及旋转中心为点B，所作图形如下：

    点评：本题考查了轴对称作图及旋转作图的知识

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （本题满分12分）如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，设DQ＝t（0≤t≤2），线段PQ的垂直平分线分别交边AD、BC于点M、N，过Q作QE⊥AB于点E，过M作MF⊥BC于点F．

    （1）当t≠1时，求证：△PEQ≌△NFM；

    （2）顺次连接P、M、Q、N，设四边形PMQN的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．

     

     

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

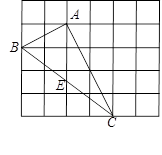
    （本题满分8分）如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：

    （1）画线段AD∥BC且使AD =BC，连接CD；

    （2）线段AC的长为      ，CD的长为     ，AD的长为       ；

    （3）△ACD为      三角形，四边形ABCD的面积为      ；

    （4）若E为BC中点，则tan∠CAE的值是    ．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    ﹣（本题10分）如图，在边长为1的小正方形组成的网格中，的三个顶点均在格点上，请按要求完成下列各题：
    （1）  用签字笔画AD∥BC（D为格点），连接CD；线段CD的长为      ；
    （2）  请你在的三个内角中任选一个锐角，若你所选的锐角是      ，则它所对应的正弦函数值是             ．
    （3） 若E为BC中点，则tan∠CAE的值是     .

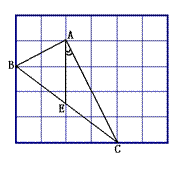
    查看答案和解析>>

    科目：初中数学 来源：2011年初中毕业升学考试（山东枣庄卷）数学 题型：解答题

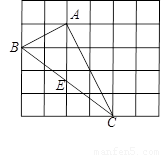
    （本题满分8分）如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：

    （1）画线段AD∥BC且使AD =BC，连接CD；

    （2）线段AC的长为       ，CD的长为      ，AD的长为        ；

    （3）△ACD为      三角形，四边形ABCD的面积为      ；

    （4）若E为BC中点，则tan∠CAE的值是     ．

     

    查看答案和解析>>

    科目：初中数学 来源：2011年初中毕业升学考试（内蒙古乌兰察布卷）数学 题型：解答题

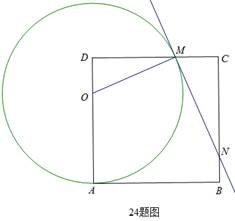
    （2011广西崇左，24，14分）（本小题满分14分）如图，在边长为8的正方形ABCD

    中，点O为AD上一动点（4＜OA＜8），以O为圆心，OA的长为半径的圆交边CD于点M，连接OM，过点M作圆O的切线交边BC于点N.

    （1）       求证：△ODM∽△MCN；[来源:学+科+网]

    （2）       设DM=x，求OA的长（用含x的代数式表示）；

    （3）       在点O运动的过程中，设△CMN的周长为p，试用含x的代数式表示p，你能发现怎样的结论？

     

    查看答案和解析>>

    同步练习册答案