
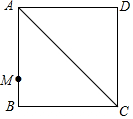
 如图,正方形ABCD的边长为8cm,点M在AB上,BM=2cm,对角线AC有一个动点P,求PM+PB的最小值.
如图,正方形ABCD的边长为8cm,点M在AB上,BM=2cm,对角线AC有一个动点P,求PM+PB的最小值. 分析 根据正方形的性质,点B、D关于AC对称,连接DM与AC相交于点P,根据轴对称确定最短路线问题,点P即为所求作的点,求出AM,然后利用勾股定理列式计算即可得解.
解答 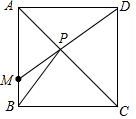 解:如图,在正方形ABCD中,点B、D关于AC对称,
解:如图,在正方形ABCD中,点B、D关于AC对称,
连接DM,与AC相交于点P,
由轴对称确定最短路线问题,点P即为所求作的PM+PB最小的点,
∵正方形ABCD的边长为8cm,BM=2cm,
∴AM=8-2=6cm,
又∵∠BAD=90°,
∴MD=$\sqrt{A{M}^{2}+A{D}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10cm.
即PM+PB的最小值10cm.
点评 本题考查了轴对称确定最短路线问题,正方形的性质,熟记性质以及最短路径的确定方法准确确定出点P的位置是解题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:填空题
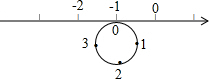 如图,圆的周长为4个单位长,数轴每个数字之间的距离为1个单位,在圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上(如圆周上表示数字3的点与数轴上表示-2的点重合…),则数轴上表示-2016的点与圆周上表示数字1的点重合.
如图,圆的周长为4个单位长,数轴每个数字之间的距离为1个单位,在圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上(如圆周上表示数字3的点与数轴上表示-2的点重合…),则数轴上表示-2016的点与圆周上表示数字1的点重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 若实数a、b、c在数轴的位置,如图所示,则化简$\sqrt{(a+c)^{2}}$-|b-c|的结果是( )
若实数a、b、c在数轴的位置,如图所示,则化简$\sqrt{(a+c)^{2}}$-|b-c|的结果是( )| A. | -a-b | B. | a-b | C. | a-b+2c | D. | -a-b-2c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $±\sqrt{16}=±4$ | B. | $(-\sqrt{2}{)^2}=4$ | C. | $\root{3}{-9}$=-3 | D. | $\sqrt{(-3{)^2}}=-3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com