
ΓΨΧβΡΩΓΩΘ®ΡΘ–ΆΫ®ΝΔΘ©
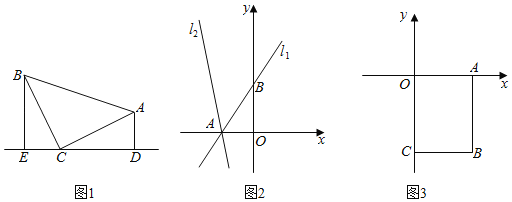
Θ®1Θ©»γΆΦ1Θ§Β»―ϋRtΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§CBΘΫCAΘ§÷±œΏEDΨ≠ΙΐΒψCΘ§ΙΐΒψAΉςADΓΆED”ΎΒψDΘ§ΙΐΒψBΉςBEΓΆED”ΎΒψEΘ§«σ÷ΛΘΚΓςBECΓ’ΓςCDAΘΜ
Θ®ΡΘ–Ά”Π”ΟΘ©
Θ®2Θ©»γΆΦ2Θ§“―÷Σ÷±œΏl1ΘΚyΘΫ![]() x+3”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ§ΫΪ÷±œΏl1»ΤΒψAΡφ ±’κ–ΐΉΣ45Γψ÷Ν÷±œΏl2ΘΜ«σ÷±œΏl2ΒΡΚ· ΐ±μ¥ο ΫΘΜ
x+3”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ§ΫΪ÷±œΏl1»ΤΒψAΡφ ±’κ–ΐΉΣ45Γψ÷Ν÷±œΏl2ΘΜ«σ÷±œΏl2ΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®3Θ©»γΆΦ3Θ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒΡΎ”–“ΜΒψBΘ®3Θ§©¹4Θ©Θ§ΙΐΒψBΉςBAΓΆx÷α”ΎΒψAΓΔBCΓΆy÷α”ΎΒψCΘ§ΒψP «œΏΕΈAB…œΒΡΕ·ΒψΘ§ΒψD «÷±œΏyΘΫ©¹2x+1…œΒΡΕ·Βψ«“‘ΎΒΎΥΡœσœόΡΎΘ° ‘ΧΫΨΩΓςCPDΡήΖώ≥…ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΩ»τΡήΘ§«σ≥ωΒψDΒΡΉχ±ξΘ§»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊœξΫβΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©ΒψDΉχ±ξΒΟΘ®
ΘΜΘ®3Θ©ΒψDΉχ±ξΒΟΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®4Θ§
Θ©ΜρΘ®4Θ§![]() 7Θ©ΜρΘ®
7Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”…¥Ι÷±ΒΡΕ®“εΒΟΓœADC=ΓœCEB=90ΓψΘ§ΤΫΫ«ΒΡΕ®“εΚΆΆ§Ϋ«ΒΡ”ύΫ«ΒΡœύΒ»«σ≥ωΓœDAC=ΓœECBΘ§Ϋ«Ϋ«±Ώ÷ΛΟςΓςCDAΓ’ΓςBECΘΜ
Θ®2Θ©÷ΛΟςΓςABOΓ’ΓœBCDΘ§«σ≥ωΒψCΒΡΉχ±ξΈΣΘ®-3Θ§5Θ©Θ§”…ΒψΒΫ÷±œΏ…œΙΙΫ®Εΰ‘Σ“Μ¥ΈΖΫ≥ΧΉι«σ≥ωk=![]() 5Θ§b=
5Θ§b=![]() 10Θ§¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏl2ΒΡΚ· ΐ±μ¥ο ΫΈΣy=-5x-10ΘΜ
10Θ§¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏl2ΒΡΚ· ΐ±μ¥ο ΫΈΣy=-5x-10ΘΜ
Θ®3Θ©ΙΙΫ®ΓςMCPΓ’ΓςHPDΘ§”…Τδ–‘÷ Θ§ΒψD‘Ύ÷±œΏy=-2x+1«σ≥ωm=![]() Μρn=0Μρ
Μρn=0Μρ![]() Θ§ΫΪmΒΡ÷Β¥ζ»κΘ§ΒΟΒψDΉχ±ξΒΟΘ®
Θ§ΫΪmΒΡ÷Β¥ζ»κΘ§ΒΟΒψDΉχ±ξΒΟΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®4Θ§
Θ©ΜρΘ®4Θ§![]() 7Θ©ΜρΘ®
7Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΫβΘΚΘ®1Θ©»γΆΦ1Υυ ΨΘΚ
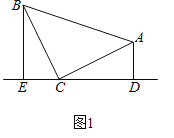
ÿADâEDȧBEâEDȧ
ΓύΓœADC=ΓœCEB=90ΓψΘ§
”÷ΓΏΓœACD+ΓœACB+ΓœBEC=180ΓψΘ§ΓœACB=90ΓψΘ§
ΓύΓœACD+ΓœBEC=90ΓψΘ§
”÷ΓΏΓœACD+ΓœDAC=90ΓψΘ§
ΓύΓœDAC=ΓœECBΘ§
‘ΎΓςCDAΚΆΓςBEC÷–Θ§
 Θ§
Θ§
ΓύΓςCDAΓ’ΓςBECΘ®AASΘ©ΘΜ
Θ®2Θ©ΙΐΒψBΉςBCΓΆABΫΜAC”ΎΒψCΘ§CDΓΆy÷αΫΜy÷α”ΎΒψDΘ§»γΆΦ2Υυ ΨΘΚ
ΓΏCDΓΆy÷αΘ§x÷αΓΆy÷αΘ§
ΓύΓœCDB=ΓœBOA=90ΓψΘ§
”÷ΓΏBCΓΆABΘ§
ΓύΓœABC=90ΓψΘ§
”÷ΓΏΓœABO+ΓœABC+ΓœCBD=180ΓψΘ§
ΓύΓœABO+ΓœCBD=90ΓψΘ§
”÷ΓΏΓœBAO+ΓœABO=90ΓψΘ§
ΓύΓœBAO=ΓœCBDΘ§
”÷ΓΏΓœBAC=45ΓψΘ§
ΓύΓœACB=45ΓψΘ§
ΓύAB=CBΘ§
‘ΎΓςABOΚΆΓœBCD÷–Θ§
 Θ§
Θ§
ΓύΓςABOΓ’ΓœBCDΘ®AASΘ©Θ§
ΓύAO=BDΘ§BO=CDΘ§
”÷ΓΏ÷±œΏl1ΘΚy=![]() x+3”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ§
x+3”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ§
ΓύΒψAΓΔBΝΫΒψΒΡΉχ±ξΖ÷±πΈΣΘ®-2Θ§0Θ©Θ§Θ®0Θ§3Θ©Θ§
ΓύAO=2Θ§BO=3Θ§
ΓύBD=2Θ§CD=3Θ§
ΓύΒψCΒΡΉχ±ξΈΣΘ®-3Θ§5Θ©Θ§
…ηl2ΒΡΚ· ΐ±μ¥ο ΫΈΣy=kx+bΘ®kΓΌ0Θ©Θ§
ΒψAΓΔCΝΫΒψ‘Ύ÷±œΏl2…œΘ§“άΧβ“βΒΟΘΚ
![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ÷±œΏl2ΒΡΚ· ΐ±μ¥ο ΫΈΣy=![]() 5x
5x![]() 10ΘΜ
10ΘΜ
Θ®3Θ©Ρή≥…ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§“άΧβ“βΒΟΘ§
ΔΌ»τΒψPΈΣ÷±Ϋ« ±Θ§»γΆΦ3ΦΉΥυ ΨΘΚ
…ηΒψPΒΡΉχ±ξΈΣΘ®3Θ§mΘ©Θ§‘ρPBΒΡ≥ΛΈΣ4+mΘ§
ΓΏΓœCPD=90ΓψΘ§CP=PDΘ§
ΓœCPM+ΓœCDP+ΓœPDH=180ΓψΘ§
ΓύΓœCPM+ΓœPDH=90ΓψΘ§
”÷ΓΏΓœCPM+ΓœDPM=90ΓψΘ§
ΓύΓœPCM=ΓœPDHΘ§
‘ΎΓςMCPΚΆΓςHPD÷–Θ§
 Θ§
Θ§
ΓύΓςMCPΓ’ΓςHPDΘ®AASΘ©Θ§
ΓύCM=PHΘ§PM=PDΘ§
ΓύΒψDΒΡΉχ±ξΈΣΘ®7+mΘ§-3+mΘ©Θ§
”÷ΓΏΒψD‘Ύ÷±œΏy=-2x+1…œΘ§
Γύ-2Θ®7+mΘ©+1=-3+mΘ§
ΫβΒΟΘΚm=![]() Θ§
Θ§
Φ¥ΒψDΒΡΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
ΔΎ»τΒψCΈΣ÷±Ϋ« ±Θ§»γΆΦ3““Υυ ΨΘΚ
…ηΒψPΒΡΉχ±ξΈΣΘ®3Θ§nΘ©Θ§‘ρPBΒΡ≥ΛΈΣ4+nΘ§
CA=CDȧ
Ά§άμΩ…÷ΛΟςΓςPCMΓ’ΓςCDHΘ®AASΘ©Θ§
ΓύPM=CHΘ§MC=HDΘ§
ΓύΒψDΒΡΉχ±ξΈΣΘ®4+nΘ§-7Θ©Θ§
”÷ΓΏΒψD‘Ύ÷±œΏy=-2x+1…œΘ§
Γύ-2Θ®4+nΘ©+1=-7Θ§
ΫβΒΟΘΚn=0Θ§
ΓύΒψP”κΒψA÷ΊΚœΘ§ΒψM”κΒψO÷ΊΚœΘ§
Φ¥ΒψDΒΡΉχ±ξΈΣΘ®4Θ§-7Θ©ΘΜ
Δέ»τΒψDΈΣ÷±Ϋ« ±Θ§»γΆΦ3±ϊΥυ ΨΘΚ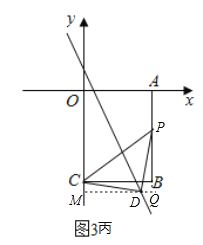
…ηΒψPΒΡΉχ±ξΈΣΘ®3Θ§kΘ©Θ§‘ρPBΒΡ≥ΛΈΣ4+kΘ§
CD=PDȧ
Ά§άμΩ…÷ΛΟςΓςCDMΓ’ΓςPDQΘ®AASΘ©Θ§
ΓύMD=PQΘ§MC=DQΘ§
ΓύΒψDΒΡΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
”÷ΓΏΒψD‘Ύ÷±œΏy=-2x+1…œΘ§
Γύ-2ΓΝ![]() +1=
+1=![]() Θ§
Θ§
ΫβΒΟΘΚk=![]() Θ§
Θ§
ΓύΒψP”κΒψA÷ΊΚœΘ§ΒψM”κΒψO÷ΊΚœΘ§
Φ¥ΒψDΒΡΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
ΉέΚœ…œ ωΘ§ΒψDΉχ±ξΒΟΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®4Θ§
Θ©ΜρΘ®4Θ§![]() 7Θ©ΜρΘ®
7Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§ΓœABDΓΔΓœCDBΒΡΤΫΖ÷œΏBEΓΔDFΖ÷±πΫΜ±ΏADΓΔBC”ΎΒψEΓΔFΘ°
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈBEDF «ΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©Β±ΓœABEΈΣΕύ…ΌΕ» ±Θ§ΥΡ±Ώ–ΈBEDF «Νβ–ΈΘΩ«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβ―ß…ζΕ‘Ης÷÷«ράύ‘ΥΕ·ΒΡœ≤Α°≥ΧΕ»Θ§–ΓΟς≤…»ΓΥφΜζ≥ι―υΒΡΖΫΖ®Ε‘ΥϊΥυ‘Ύ―ß–ΘΒΡ≤ΩΖ÷―ß…ζΫχ––Έ ΨμΒς≤ιΘ®ΟΩΗω±ΜΒς≤ιΒΡ―ß…ζ±Ί–κ―Γ‘ώΕχ«“÷ΜΡή―Γ‘ώΤδ÷–“Μ÷÷œνΡΩΘ©Θ§Ε‘Βς≤ιΫαΙϊΫχ––Ά≥ΦΤΚσΘ§Μφ÷ΤΝΥœ¬ΟφΒΡΆ≥ΦΤΆΦΘ®1Θ©ΚΆΆΦΘ®2Θ©Θ°


Θ®1Θ©¥Υ¥Έ±ΜΒς≤ιΒΡ―ß…ζΙ≤”–___»ΥΘ§mΘΫ_____ΘΜ
Θ®2Θ©«σœ≤ΜΕΓΑΤΙ≈“«ρΓ±ΒΡ―ß…ζΒΡ»Υ ΐΘ§≤ΔΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©»τΗΟ–Θ”–2000Οϊ―ß…ζΘ§ΙάΦΤ»Ϊ–Θœ≤ΜΕΓΑΉψ«ρΓ±ΒΡ―ß…ζ¥σ‘Φ”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΒ»±ΏΓςABC÷–Θ§D «±ΏAC…œ“ΜΒψΘ§Ν§Ϋ”BDΘ§ΫΪΓςBCD»ΤΒψBΡφ ±’κ–ΐΉΣ60ΓψΘ§ΒΟΒΫΓςBAEΘ§Ν§Ϋ”EDΘ§œ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ”–Θ®ΓΓΓΓΘ©ΗωΘ°
ΔΌΓςBED «Β»±Ώ»ΐΫ«–ΈΘΜΔΎAEΓΈBCΘΜ ΔέΓςADEΒΡ÷ή≥ΛΒ»”ΎBD+BCΘΜΔήΓœADEΘΫΓœDBCΘ°
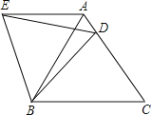
A.1B.2C.3D.4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©«σ÷ΛΘΚ»ΐΫ«–Έ»ΐΗωΡΎΫ«ΒΡΚΆΒ»”Ύ180ΓψΘ°
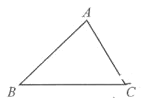
Θ®2Θ©‘ΡΕΝ≤ΡΝœ≤ΔΜΊ¥πΈ ΧβΘΚ
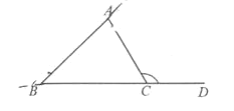
»γΆΦΘ§Α―ΓςABCΒΡ“Μ±ΏBC―”≥ΛΘ§ΒΟΒΫΓœACDΘ°œώ’β―υΘ§»ΐΫ«–ΈΒΡ“Μ±Ώ”κΝμ“Μ±ΏΒΡ―”≥ΛœΏΉι≥…ΒΡΫ«Θ§Ϋ–Ήω»ΐΫ«–ΈΒΡΓΑΆβΫ«Γ±Θ§‘ΎΟΩΗωΕΞΒψ¥Π»Γ’βΗω»ΐΫ«–ΈΒΡ“ΜΗωΆβΫ«Θ§ΥϋΟ«ΒΡΚΆΫ–Ήω’βΗω»ΐΫ«–ΈΒΡΓΑΆβΫ«ΚΆΓ±Θ°≤Ι»ΪΆΦ–Έ≤Δ«σΓςABCΒΡΓΑΆβΫ«ΚΆΓ±Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
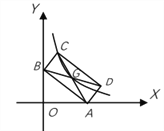
ΓΨΧβΡΩΓΩ»γΆΦ,ΨΊ–ΈABCDΒΡΝΫΗωΕΞΒψAΓΔBΖ÷±π¬δ‘ΎxΓΔy÷α…œ,ΕΞΒψCΓΔDΈΜ”ΎΒΎ“Μœσœό,«“OA=3,OB=2,Ε‘Ϋ«œΏACΓΔBDΫΜ”ΎΒψG,»τ«ζœΏy![]() Ψ≠ΙΐΒψCΓΔGΘ§‘ρk=__________.
Ψ≠ΙΐΒψCΓΔGΘ§‘ρk=__________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ±Ώ≥ΛΈΣ4ΒΡΒ»±Ώ![]() ”κΒ»±Ώ
”κΒ»±Ώ![]() ΜΞœύ÷ΊΚœΘ§ΫΪ
ΜΞœύ÷ΊΚœΘ§ΫΪ![]() ―Ί÷±œΏLœρΉσΤΫ“ΤmΗωΒΞΈΜ≥ΛΕ»Θ§ΫΪ
―Ί÷±œΏLœρΉσΤΫ“ΤmΗωΒΞΈΜ≥ΛΕ»Θ§ΫΪ![]() œρ”““≤ΤΫ“ΤmΗωΒΞΈΜ≥ΛΕ»Θ§»τ
œρ”““≤ΤΫ“ΤmΗωΒΞΈΜ≥ΛΕ»Θ§»τ![]() Θ§‘ρm=________ΘΜ»τCΓΔE «œΏΕΈBFΒΡ»ΐΒ»Ζ÷Βψ ±Θ§m=________.
Θ§‘ρm=________ΘΜ»τCΓΔE «œΏΕΈBFΒΡ»ΐΒ»Ζ÷Βψ ±Θ§m=________.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΙέ≤λœ¬Ν–“ΜΉιΆΦ–Έ÷–ΒψΒΡΗω ΐΘ§Τδ÷–ΒΎ1ΗωΆΦ÷–Ι≤”–4ΗωΒψΘ§ΒΎ2ΗωΆΦ÷–Ι≤”–10ΗωΒψΘ§ΒΎ3ΗωΆΦ÷–Ι≤”–19ΗωΒψΘ§Γ≠Θ§Α¥¥ΥΙφ¬…ΒΎ6ΗωΆΦ÷–Ι≤”–ΒψΒΡΗω ΐ «Θ®ΓΓΓΓΘ©
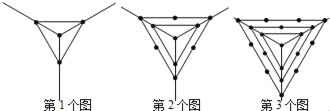
A.46B.63C.64D.73
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΑ―œ¬Ν–Εύœν ΫΖ÷Ϋβ“ρ Ϋ
Θ®1Θ© 8a3b2-12ab3c Θ®2Θ©2x3Θ≠4x2ΘΪ2x Θ®3Θ©![]() Θ®4Θ©Θ®ab+aΘ©+Θ®b+1Θ© Θ®5Θ©
Θ®4Θ©Θ®ab+aΘ©+Θ®b+1Θ© Θ®5Θ©![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com