
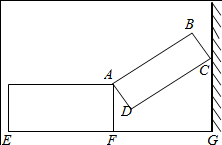
 如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.
如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.分析 (1)如图,过点B作BH⊥CG于H,过点D作CG的垂线MN交AF于M,交HG于N.利用矩形的性质、直角三角形的性质以及等角的余角相等得到∠MAD=30°,根据周角的定义易求箱盖绕点A转过的角度;通过解直角△BHC来求BH的长度;
(2)通过解直角△AMD得到线段MD的长度,则DN=65-EF-DM,利用解直角△DCN来求CD的长度,即EF的长度即可.
解答 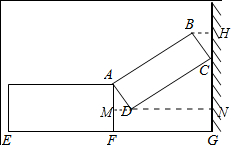 解:(1)如图,过点B作BH⊥CG于H,过点D作CG的垂线MN交AF于M,交HG于N.
解:(1)如图,过点B作BH⊥CG于H,过点D作CG的垂线MN交AF于M,交HG于N.
∵∠DCG=60°,
∴∠CDN=30°.
又∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,
∴∠MAD=∠CDN=30°(同角的余角相等),
∴箱盖绕点A转过的角度为:360°-90°-30°-90°=150°.
在直角△BCH中,∠BCH=30°,BC=10cm,则BH=$\frac{1}{2}$BC=5cm.
故答案是:150°;5;
(2)在直角△AMD中,AD=BC=10cm,∠MAD=30°,则MD=AD•sin30°=$\frac{1}{2}$×10=5(cm).
∵∠DCN=30°,
∴cos∠DCN=cos30°=$\frac{DN}{DC}$=$\frac{65-EF-5}{EF}$,即$\frac{65-EF-5}{EF}$=$\frac{\sqrt{3}}{2}$,
解得EF=32.4.
即箱子的宽EF是32.4cm.
点评 本题考查了解直角三角形的应用.主要是余弦概念及运算,关键把实际问题转化为数学问题加以计算.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 27cm2 | B. | 18cm2 | C. | $\frac{27}{4}c{m^2}$ | D. | $\frac{27}{2}c{m^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
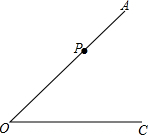 画图并回答:
画图并回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
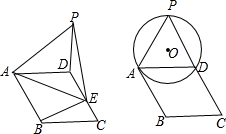 已知:如图?ABCD中,CD=CB=3,∠C=60°,点E是CD边上自C向D的动点(点E到点D停止运动),连结AE,以AE为边作等边△AEP,连结DP.
已知:如图?ABCD中,CD=CB=3,∠C=60°,点E是CD边上自C向D的动点(点E到点D停止运动),连结AE,以AE为边作等边△AEP,连结DP.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
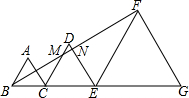 如图,△ABC、△DCE、△FEG为等边三角形,边长分别为2、3、5,且从左至右如图排列,连接BF,交DC、DE分别于M、N两点,则△DMN的面积为$\frac{\sqrt{3}}{8}$.
如图,△ABC、△DCE、△FEG为等边三角形,边长分别为2、3、5,且从左至右如图排列,连接BF,交DC、DE分别于M、N两点,则△DMN的面积为$\frac{\sqrt{3}}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
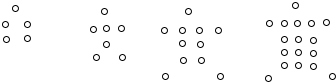
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
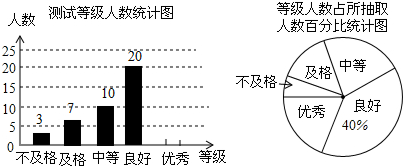
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m+n≥1 | B. | m+n≤1 | C. | m+n≥$\frac{1}{2}$ | D. | m+n≤$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com