
”¾ĢāÄæ”æČō½«Ņ»øö×ŌČ»Źżø÷Ī»ÉĻµÄŹż×Ö°“ÕÕ“ÓøßĪ»Źż×Öµ½µĶĪ»Źż×ÖÅųÉŅ»ĮŠŗó£¬ŗóŅ»øöČĖŹż¼õČ„Ē°Ņ»øöŹżµÄ²īŹĒŅ»øö³£Źż£¬ŌņÕāøöŹż½Š×ö”°ŠŅø£Źż”±.Čē£ŗĖÄĪ»Źż2468ÅųÉŅ»ĮŠŗóĪŖ£ŗ2,4,6,8.ŅņĪŖ8-6=6-4=4-2=2£¬ĒŅ²īĪŖ2µÄ³£Źż£¬¹Ź2468ŹĒŅ»øö²īĪŖ2µÄĖÄĪ»”°ŠŅø£Źż”±.ÓÖČē£¬9876,6666µČŅ²ŹĒ”°ŠŅø£Źż”±.
ČōŅ»øö×ŌČ»Źż“Ó×óµ½ÓŅø÷ŹżĪ»ÉĻµÄŹż×ÖŗĶĮķŅ»øö×ŌČ»Źż“ÓÓŅµ½×óø÷ŹżĪ»ÉĻµÄŹż×ÖĶźČ«ĻąĶ¬£¬Ōņ³ĘÕāĮ½øöŹżĪŖ”°ČżÉśČżŹĄŹż”±.ĄżČē£ŗ3579Óė9753,8765Óė5678£¬...£¬¶¼ŹĒ”°ČżÉśČżŹĄŹż”±.
¹ę¶Ø£ŗ°ŃøßĪ»Źż×ÖĪŖx£¬²īĪŖ2µÄČżĪ»”°ŠŅø£Źż”±ÓėĖüµÄ”°ČżÉśČżŹĄŹż”±µÄŗĶÓė222µÄÉĢ¼ĒĪŖF(x).ĄżČēµ±x=5Ź±£¬ČżĪ»”°ŠŅø£Źż”±ĪŖ579£¬ĖüµÄ”°ČżÉśČżŹĄŹż”±ĪŖ975£¬ČżĪ»”°ŠŅø£Źż”±ÓėĖüµÄ”°ČżÉśČżŹĄŹż”±µÄŗĶĪŖ£ŗ579+975=1554,1554”Ā222=7£¬ĖłŅŌF(x)=7.
£Ø1£©¼ĘĖć£ŗF(1), F(4)£»
£Ø2£©ŅŃÖŖF(x) =4£¬ĒóxµÄÖµ.
”¾“š°ø”æ£Ø1£©F(1) =3£¬F(4) =6£»(2) x=2.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻĢāŅāæɵƔ°ŠŅø£Źż”±Óė”°ČżÉśČżŹĄŹż”±£¬Č»ŗó°“Ėł¹ę¶ØµÄŌĖĖćĖ³Šņ½ųŠŠ¼ĘĖć¼“æÉµĆ£»
£Ø2£©ÉčČżĪ»ŹżµÄ×īøßĪ»ĪŖx£¬øł¾Ż¶ØŅå±ķŹ¾³ö”°ŠŅø£Źż”±Óė”°ČżÉśČżŹĄŹż”±£¬Č»ŗó°“¹ę¶ØµÄŌĖĖćĖ³ŠņĮŠ³ö·½³Ģ£¬½ā·½³Ģ¼“æɵĆ.
ŹŌĢā½āĪö£ŗ£Ø1£©ÓÉĢāæÉÖŖ£¬
µ±x=1Ź±£¬”°ŠŅø£Źż”±£ŗ135£»”°ČżÉśČżŹĄŹż”±£ŗ531
F(1)=£Ø135+531£©”Ā222=3£»
Ķ¬ĄķæÉµĆ£¬µ±x=4Ź±£¬”°ŠŅø£Źż”±£ŗ468£»”°ČżÉśČżŹĄŹż”±£ŗ864
F(4)=£Ø468+864£©”Ā222=6£»
(2)ÉčČżĪ»ŹżµÄ×īøßĪ»ĪŖx£¬Ōņ
”°ŠŅø£Źż”±£ŗ100x+10£Øx+2£©+£Øx+4£©£»”°ČżÉśČżŹĄŹż”±£ŗ100£Øx+4£©+10£Øx+2£©+x
ÓÖ ![]() F(x) =4£¬
F(x) =4£¬
![]() £ū[100x+10£Øx+2£©+£Øx+4£©]+[100£Øx+4£©+10£Øx+2£©+x]£ż”Ā222=4£¬
£ū[100x+10£Øx+2£©+£Øx+4£©]+[100£Øx+4£©+10£Øx+2£©+x]£ż”Ā222=4£¬
½āµĆ£¬x=2.


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ńÄź£¬ĪŅ¹śÕžø®ĪŖ¼õĒįÅ©Ćńøŗµ££¬¾ö¶ØŌŚ 5 ğČĆāČ„Å©ŅµĖ°£®Ä³Ļē½ńÄźČĖ¾łÉĻ½ÉÅ©ŅµĖ° 25 ŌŖ£¬ČōĮ½ÄźŗóČĖ¾łÉĻ½ÉÅ©ŅµĖ°ĪŖ 16 ŌŖ£¬¼ŁÉčÕāĮ½Äź½µµĶµÄ°Ł·ÖĀŹĻąĶ¬
£Ø1£©Ēó½µµĶµÄ°Ł·ÖĀŹ£»
£Ø2£©Š”ŗģĖłŌŚµÄĻēŌ¼ÓŠ 16000 Å©Ćń£¬ĪŹøĆĻēÅ©ĆńĆ÷Äź¼õÉŁ¶ąÉŁÅ©ŅµĖ°£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
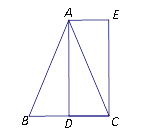
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬ ![]() £¬
£¬ ![]() ÓŚµć
ÓŚµć![]() £¬°ŃĻ߶Ī
£¬°ŃĻ߶Ī![]() ŃŲ×Å
ŃŲ×Å![]() µÄ·½ĻņĘ½ŅĘ
µÄ·½ĻņĘ½ŅĘ![]() µĆµ½Ļ߶Ī
µĆµ½Ļ߶Ī![]() £¬Į¬½Ó
£¬Į¬½Ó![]() .
.
ĪŹ£ŗ(1)ĖıߊĪ![]() ŹĒ_________ŠĪ£»
ŹĒ_________ŠĪ£»
(2)Čō![]() µÄÖܳ¤±Č
µÄÖܳ¤±Č![]() µÄÖܳ¤“ó6£¬ĒóĖıߊĪ
µÄÖܳ¤“ó6£¬ĒóĖıߊĪ![]() µÄĆ껿.
µÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÅŹÖ¦»ØĆ¢¹ūÓÉÓŚĘ·ÖŹøß”¢æŚøŠŗƶųĪÅĆūČ«¹ś£¬ĶعżÓÅÖŹæģ½ŻµÄĶųĀēĻśŹŪĒžµĄ£¬Š”Ć÷µÄĀčĀčĻČ¹ŗĀņĮĖ2ĻäAĘ·ÖÖĆ¢¹ūŗĶ3ĻäBĘ·ÖÖĆ¢¹ū£¬¹²»Ø·Ń450ŌŖ£»ŗóÓÖ¹ŗĀņĮĖlĻäAĘ·ÖÖĆ¢¹ūŗĶ2ĻäBĘ·ÖÖĆ¢¹ū£¬¹²»Ø·Ń275ŌŖ£ØĆæ“ĪĮ½ÖÖĆ¢¹ūµÄŹŪ¼Ū¶¼²»±ä£©£®
£Ø1£©ĪŹAĘ·ÖÖĆ¢¹ūŗĶBĘ·ÖÖĆ¢¹ūµÄŹŪ¼Ū·Ö±šŹĒĆæĻ䶹ɣŌŖ£æ
£Ø2£©ĻÖŅŖ¹ŗĀņĮ½ÖÖĆ¢¹ū¹²18Ļ䣬ŅŖĒóBĘ·ÖÖĆ¢¹ūµÄŹżĮæ²»ÉŁÓŚAĘ·ÖÖĆ¢¹ūŹżĮæµÄ2±¶£¬µ«²»³¬¹żAĘ·ÖÖĆ¢¹ūŹżĮæµÄ4±¶£¬ĒėÄćÉč¼Ę¹ŗĀņ·½°ø£¬²¢Š“³öĖłŠč·ŃÓĆ×īµĶµÄ¹ŗĀņ·½°ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚČż½ĒŠĪµÄÖŠĻߣ¬øßĻߣ¬½ĒĘ½·ÖĻßÖŠ£¬Ņ»¶ØÄÜ°ŃČż½ĒŠĪµÄĆ껿µČ·ÖµÄŹĒ_______.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĖÄøöŹż©3£¬0£¬1£¬2£¬ĘäÖŠøŗŹżŹĒ£Ø””””£©
A.©3
B.0
C.1
D.2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōµćP£Ø3£¬b£©ŌŚµŚĖÄĻóĻŽÄŚ£¬ŌņµćQ£Øb£¬©3£©ĖłŌŚĻóĻŽŹĒ£Ø””””£©
A. µŚŅ»ĻóĻŽ B. µŚ¶žĻóĻŽ C. µŚČżĻóĻŽ D. µŚĖÄĻóĻŽ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖyŹĒxµÄŅ»“ĪŗÆŹż£¬ĒŅµ±x=©4Ź±£¬y=9£»µ±x=6Ź±£¬y=©1£®
£Ø1£©ĒóÕāøöŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©µ±x=© ![]() Ź±£¬ŗÆŹżyµÄÖµ£»
Ź±£¬ŗÆŹżyµÄÖµ£»
£Ø3£©µ±y£¼1Ź±£¬×Ō±äĮæxȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com