精英家教网 > 初中数学 > 题目详情

在△ABC中，如果三边满足AC²=AB²-BC²，则∠A+∠B=________．

90°
分析：先把AC²=AB²-BC²，转化为AB²=AC²+BC²的形式，再由勾股定理的逆定理可判断出△ABC是直角三角形，再根据大边对大角的性质得出∠C=90°，然后根据三角形内角和定理即可作答．
解答：∵AC²=AB²-BC²，
∴AB²=AC²+BC²，
∴△ABC是直角三角形，
∴∠C=90°，
∴∠A+∠B=90°．
故答案为90°．
点评：本题主要考查的是勾股定理的逆定理，即果三角形的三边长a，b，c满足a²+b²=c²，那么这个三角形就是直角三角形．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：阅读理解

阅读材料，解答问题．
已知：锐角△ABC，如图，求作：正方形DEFG，使D、E落在BC边上，F、G分别落在AC、AB边上．
作法：（1）画一个有三个顶点落在△ABC两边上的正方形D₁、E₁、F₁、G₁（如图所示）；
（2）连接BF，并延长交AC于点F；
（3）过点F作EF⊥BC于点E；
（4）过F作FG∥BC，交AB于点G；
（5）过点G作GD⊥BC于点D；则四边形DEFG即为所求作的正方形．
问题：（1）说明上述所求作四边形DEFG为正方形的理由．
（2）在△ABC中，如果BC=120，BC边上的高为80，求上述正方形DEFG的边长．
（3）若把（2）中的正方形DEFG改为矩形DEFG，且GF=

DG，其他条件不变，此时，GF是多少？

查看答案和解析>>

科目：初中数学 来源：活学巧练　　八年级数学　　下 题型：013

下列说法中错误的是

[　　]

A．在△ABC中，设三个内角中最小的角为α，则＜α≤

B．在△ABC中，三个内角度数之比为1∶2∶3，则这个三角形是直角三角形

C．在△ABC中，如果∠B＝∠C＝，则此三角形为锐角三角形

D．在△ABC的内角中，锐角的个数最多

查看答案和解析>>

科目：初中数学 来源：2006年初中数学总复习下册 题型：022

如图所示，在△ABC中，如果AB＝30 cm，BC＝24 cm，CA＝27 cm，AE＝EF＝FB，EG∥DF∥BC，FM∥EN∥AC，图中阴影部分三个三角形周长的和为________．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

阅读材料，解答问题．
已知：锐角△ABC，如图，求作：正方形DEFG，使D、E落在BC边上，F、G分别落在AC、AB边上．
作法：（1）画一个有三个顶点落在△ABC两边上的正方形D₁、E₁、F₁、G₁（如图所示）；
（2）连接BF，并延长交AC于点F；
（3）过点F作EF⊥BC于点E；
（4）过F作FG∥BC，交AB于点G；
（5）过点G作GD⊥BC于点D；则四边形DEFG即为所求作的正方形．
问题：（1）说明上述所求作四边形DEFG为正方形的理由．
（2）在△ABC中，如果BC=120，BC边上的高为80，求上述正方形DEFG的边长．
（3）若把（2）中的正方形DEFG改为矩形DEFG，且GF= $数学公式$ DG，其他条件不变，此时，GF是多少？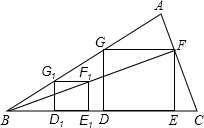

查看答案和解析>>

科目：初中数学 来源：广东省月考题 题型：解答题

阅读材料，解答问题。
已知：锐角△ABC，如图，求作：正方形DEFG，使D、E落在BC边上，F、G分别落在AC、AB边上。
作法：
（1）画一个有三个顶点落在△ABC两边上的正方形D₁、E₁、F₁、G₁（如图所示）；
（2）连结BF，并延长交AC于点F；
（3）过点F作EF⊥BC于点E；
（4）过F作FG//BC，交AB于点G；
（5）过点G作GD⊥BC于点D；则四边形DEFG即为所求作的正方形。
问题：（1）说明上述所求作四边形DEFG为正方形的理由。
（2）在△ABC中，如果BC=120，BC边上的高为80，求上述正方形DEFG的边长；
（3）若把（2）中的正方形DEFG改为矩形DEFG，且GF=

DG，其他条件不变，此时，GF是多少？

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学

在△ABC中，如果三边满足AC2=AB2-BC2，则∠A+∠B=________．

在△ABC中，如果三边满足AC²=AB²-BC²，则∠A+∠B=________．