
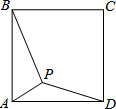
 已知:P为正方形ABCD内一点,△ABP绕点A顺时针旋转后得到的△ADM.
已知:P为正方形ABCD内一点,△ABP绕点A顺时针旋转后得到的△ADM.分析 (1)根据题意可得△ADM是△ABP绕点A顺时针旋90°后得到的,继而可画出图形;
(2)由旋转的性质,可得:∠PAM=∠BAD=90°,PA=PM,则可得△APM是等腰直角三角形;
(3)由勾股定理的逆定理,易证得△MPD是直角三角形,继而求得答案.
解答 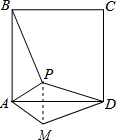 解:(1)如图,△ADM是△ABP绕点A顺时针旋90°后得到的.
解:(1)如图,△ADM是△ABP绕点A顺时针旋90°后得到的.
(2)△APM是等腰直角三角形.
理由:∵四边形ABCD是正方形,
∴∠BAD=90°,
根据旋转的性质:∠PAM=∠BAD=90°,PA=PM,
∴△APM是等腰直角三角形;
(3)∵在Rt△PAM中,AM=PA=1,∠APM=45°,
∴PM2=AM2+PA2=2,
∵由旋转的性质:PD=$\sqrt{7}$,DM=PB=3,
∴PM2+PD2=DM2,
∴∠MPD=90°,
∴∠APD=∠APM+∠MPD=45°+90°=135°.
点评 此题考查了旋转的性质、正方形的性质以及勾股定理的逆定理.注意证得△APM是等腰直角三角形,△MPD是直角三角形是关键.


科目:初中数学 来源: 题型:解答题
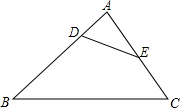 如图,在△ABC中,AC=4,AB=5,BC=6,点D、E分别在AB、AC上,且∠AED=∠B,如果四边形BCED的周长为13,求DE的长.
如图,在△ABC中,AC=4,AB=5,BC=6,点D、E分别在AB、AC上,且∠AED=∠B,如果四边形BCED的周长为13,求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
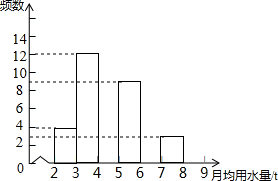 旬阳县在实施定额用水管理前,对城镇6000户居民生活用月均用水情况(单位:t)进行了简单随机抽样调查,并将调查结果绘制成频数分布表和频数分布直方图.
旬阳县在实施定额用水管理前,对城镇6000户居民生活用月均用水情况(单位:t)进行了简单随机抽样调查,并将调查结果绘制成频数分布表和频数分布直方图.| 月均用水量 | 频数 | 百分比 |
| 2≤x<3 | 4 | 8% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 14 | 28% |
| 5≤x<6 | 9 | 18% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
| 合计 | 50 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
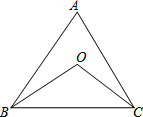 如图,点0是△ABC的∠ABC、∠ACB的平分线的交点,
如图,点0是△ABC的∠ABC、∠ACB的平分线的交点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com